El matemático C. H. Hardy dedicó parte de su vida a intentar resolver la hipótesis de Riemann (la esbozaré más adelante), hizo progresos pero nunca consiguió su propósito. Creo que fue él (y si fue otro también me vale) quien dijo que cuando era joven soñaba con resolverla; con los años se convenció de que él no lo haría pero tenía la esperanza de que a lo largo de su vida algún brillante matemático sí lo conseguiría (quizás estaba pensando en su protegido, el genial e inclasificable indio Ramanujan). Aún en el otoño de su vida seguía creyendo que quizás en el cielo sabrían la solución; próxima su muerte dudaba de que así fuese. Se suicidó en 1947, a los 70 años. Tal vez la impaciencia por comprobar si en el infierno tenían la solución se cruzó por su camino.
Otro matemático más brillante aún si cabe, David Hilbert, manifestó que si después de 500 años resucitase lo primero que haría es preguntar si se había resuelto la dichosa hipótesis. Hilbert además de por su obra matemática es famoso pues en el congreso de matemáticas de París de 1900 le impuso como tarea a los matemáticos la resolución de 23 problemas (diez en una conferencia y el resto los dejó por escrito) para resolver en el siglo XX. Quedan pocos sin solución; de ellos el más famoso es la hipótesis (o conjetura) de Riemann. A modo de aperitivo para introducir la hipótesis de Riemann (que desde ahora llamará HR) Hilbert propone otro problema, la conjetura de Goldbach: cualquier número par mayor que 2 se puede escribir como la suma de dos números primos. Hay una divertida novela sobre esta conjetura (El tío Petros y la conjetura de Goldbach de Apostolos Doxiadis).
Bueno, nos metemos en harina. La hipótesis de Riemann se puede enunciar de varias formas equivalentes. La que más me gusta es la que dice:
La parte real de cualquier cero no trivial de la función zeta de Riemann es ½.
Los que tengan claro lo que significa lo anterior lo mejor es que no perdáis el tiempo leyendo este articulito. Ir al vínculo donde se presenta formalmente el problema e intentad resolverlo. Pertenece a los denominados “siete problemas del milenio” que un millonario (Landon T. Clay) a través de su fundación, ha dotado la resolución de cada uno con un premio de un millón de dólares.
Claro que uno puede ser tan chulo como Perelman (el único que he resuelto uno de estos problemas: la conjetura de Poincaré) que sin ser de Bilbao dijo (quizás no es literal la cita que sigue):“¡Un millón de dólares!, por eso ni me molesto en ir a recogerlo” y ahí está la fundación Clay sin saber qué hacer con el dinero.
En el fondo estoy de acuerdo con Perelman (aunque yo sí habría recogido el premio): lo más importante es el orgullo de ser el más listo de la clase pues después de más de 150 años (la HR fue propuesta en 1859) uno habrá sido capaz de triunfar en lo que varias de las mentes más maravillosas (incluido Nash, el del libro y película “Una mente maravillosa”) han fracasado. Aunque lo más probable es que, con mucha suerte, acabeis encontrando alguna de las decenas de demostraciones “verdaderas” de la hipótesis que todas las semanas llegan a alguna revista prestigiosa de matemáticas pero estoy seguro que aún en ese caso os divertiréis y aprenderéis mucho.
Esto lo digo especialmente pensando en los jóvenes para los que me viene a la cabeza el discurso de Kennedy cuando anunció su intención de que los americanos fuesen a la Luna diciendo: “Elegimos ir a la luna en esta década …, no porque sean metas fáciles, sino porque son difíciles, porque ese desafío servirá para organizar y medir lo mejor de nuestras energías y habilidades, …”. El reto fue asumido por los estadounidenses y en menos de 10 años lo consiguieron (a pesar de lo que digan algunas mentes calenturientas conspiranoicas, entusiastas de Cuarto Milenio).
Para los menos ambiciosos que, como yo, se conforman con ser aficionadillos a las matemáticas (también puede ser útil para los niños) voy a intentar que oláis el problema. Usaré algunas formulas, pero pocas, además no pasa nada si no se entienden bien. Repitamos el enunciado:
“La parte real de cualquier cero no trivial de la función zeta de Riemann es ½”
Empecemos por: “La parte real”. Los matemáticos son aficionados a utilizar palabras comunes con significados muy distintos al lenguaje habitual. Así clasifican los número en naturales que son: 0, 1, 2, 3, … hasta que uno se canse y después lo retoma, pues nunca acaban. Se llaman naturales, n, pues uno los entiende de forma natural, sin mucha explicación, se ha probado que hasta los pájaros saben (hasta 4, como algunos humanos; hay otros que con más de 2 se arman tal lío que simplifican: 1,2 y muchos). Después añadieron los enteros negativos (probablemente para contabilizar las deudas): -1, -2, -3, … Más tarde se añadieron los racionales, no es que fuesen más inteligentes o equilibrados que los naturales, es que se pueden expresar como la razón, que es sinónimo de cociente o división, entre dos números, por ejemplo: 2/3, 3/5, -3/7 etc. De hecho los enteros están comprendidos en los racionales (ejemplo: 1 = 2/2, 2 = 4/2, 3= 6/2, etc.).
Uno podría pensar que cualquier número puede obtenerse operando con números racionales; pues bien el genial griego Euclides, en el siglo III antes de Cristo, se dio cuenta que la raíz de dos no hay forma de obtenerla como la razón de dos números. Esto no es nada evidente: Por ejemplo, calculemos la raíz cuadrada de dos con cinco decimales (nos vale cualquier calculadora); se obtiene: 1,41421, que puede expresarse como 141421/100000, podemos ir añadiendo decimales y aparentemente siempre encontramos una aproximación como cociente entre dos números: 141421…/100000…, pero nunca llegaremos a encontrar una solución exacta, necesitaríamos infinitos decimales, y el infinito no acaba nunca.A este tipo de números se les llaman irracionales, cuyo significado no es la primera acepción del diccionario de la RAE de irracional: “que carece de razón”, es la última: “que no puede expresarse exactamente con números enteros ni fraccionarios”.
Dentro de los irracionales hay unos muy especiales: los trascendentes, que no tienen absolutamente nada que ver con la primera acepción de trascender del DRAE (“Exhalar olor tan vivo y subido, que penetra y se extiende a gran distancia”), simplemente diré que trascendente es el número π (ver en NAUKAS mi artículo: ¿Está el Quijote escrito en π (Pi)?, para más detalles), el numero e y algunos más.
Hay muy pocos números que se haya demostrado que sean trascendentes (ahora me doy cuenta que no sé si se ha demostrado si existen infinitos trascendentes, eso lo dejo para otro día). Al conjunto de los números racionales (que incluyen los enteros) más los irracionales (que incluyen los trascendentes) se les llama números reales: podemos representarlos por una línea recta, cada número sería un punto y como un punto es tan pequeño como queramos de forma que en cualquier segmento de la recta tenemos infinitos números.
Bueno pues ya sabemos qué significa “real”, pero la definición dice “La parte real”, por tanto, deben existir entre los números partes que no son reales. Así es, es lo que se llaman números imaginarios. Si buscamos en el DRAE española la primera acepción de imaginario dice: “que solo existe en la imaginación”. No nos vale esta definición pues podríamos también aplicarla a número real. Veamos la última acepción del DRAE para imaginario: “Soldado que presta estos servicios. Una imaginaria”. Esto es muy difícil de explicar para los que tienen menos de 30 años, lo intento: antes casi todo el mundo iba obligatoriamente al ejército (se decía “ir a la mili”) cuando se tenían 20 años, o por ahí, y de vez en cuando, por huevos (DRAE: “por fuerza, necesariamente”) había que hacer una guardia toda la noche, eso era estar de imaginaria. Pues bien: las imaginarias eran muy reales, lo mismo le ocurren a los números imaginarios: son tan reales como los reales.
Pondré un ejemplo de número imaginario: no tiene solución en los números reales pues no hay ningún número real que elevado al cuadrado de -1, por ello se inventó el número i (de imaginario) para el que i2 = -1. Con esta idea vemos que .
La combinación de un número real y uno imaginario forman un número complejo, que se escribe a + b i (ejemplo: 3 + 2 i, donde 3 es la parte real y 2 i la imaginaria). Podemos decir que los complejos abarcan a los reales y a los imaginarios. Vimos que un número real se representaba por un punto en una recta. Un número complejo z se representa como como un punto sobre un plano (sobre el eje horizontal se toma la coordenada de la parte real y sobre el vertical la coordenada de la parte imaginaria, como se muestra en la siguiente figura). Espero ya queda claro lo que significa “la parte real”.
A propósito, los números complejos tienen interesantes propiedades, en las que no voy a entrar, simplemente indicar que su uso simplifica sustancialmente los cálculos de circuitos eléctricos y el tratamiento de ondas y muchas cosas más (la telefonía móvil, TV, microprocesadores, motores eléctricos le deben mucho a los números complejos)
Sigamos con la definición dice: cero no trivial. Los matemáticos suelen llamar trivial a alguna operación matemática con la que después de romperse la cabeza varias horas les queda muy clara (lo de unas horas a veces es una subestimación, por ejemplo: un Wiles, en su demostración del teorema de Fermat, un paso lo dio por trivial, cuando se le pidió que lo aclarase necesito tres años y la ayuda de otro matemático para demostrarlo, entonces todos los matemáticos estuvieron conformes con que el paso era trivial y aceptaron que la demostración de Wiles era correcta (habían pasado más de tres siglos desde que fue propuesto).
Más adelante volveremos a lo de ¡cero no trivial!, antes tengo que escribir la función zeta (ζ, en griego) de Riemann (¡qué nadie se asuste!):
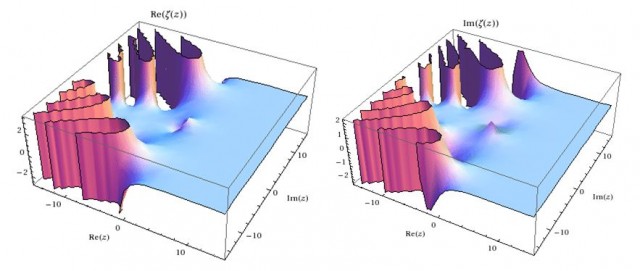
Pero el interés de esta función radica cuando s es un número complejo, que llamamos z, esto z = a + b i, que se indica , a = Re(z) y b = Im(z) (recordemos que un número real también es complejo; eso sí: un complejo que no tiene parte imaginaria). Entonces al calcular ζ(z) = ζ(a + b i) para un valor de a y b concreto obtendremos como resultado un número complejo, que tendrá una parte real, que denotamos Re(ζ(z)) y una parte imaginaria que llamamos Im(ζ(z). Hacer este cálculo no es sencillo, realmente es complicado, pero afortunadamente hay programas que lo hacen por nosotros (en mi caso uso Mathematica). Variando a entre -15 y 15 y b entre 0 y 15 representamos la parte real e imaginaria de ζ(z), que representamos por separado, obteniendo las gráficas que siguen.
En las gráficas se puede ver que hay puntos para los que ζ(z) = 0. Haciendo los cálculos se puede comprobar que ζ(z) es cero para z = -2, z = -4, o por cualquier número par negativo, esto es z = – 2n (demostrar esto no es inmediato, requiere hacer uso de un concepto de análisis complejo denominado prolongación analítica cuya explicación excede lo que aquí se quiere contar). A estos valores de z = -2 n, en los que ζ(z) = 0 se denominan ceros triviales (no os preocupéis si no os queda claro, recordad que para un matemático llegar a la conclusión de que algo es trivial le lleva su tiempo). Los ceros no triviales son otros valores de z distintos de – 2 n para los que ζ(z) es cero. Riemann conjeturó que, además de para z = -2 n, que los otros valores que hacían ζ(z) = 0, que llamamos ceros no triviales, requieren que z = 1/2 + i b , es decir que la parte real de z valga ½ (observe que es la ecuación de una recta, por tanto todos los ceros están alineados en esta recta) . Lo anterior puede decirse de otra forma “La parte real de cualquier cero no trivial de la función zeta de Riemann es ½” que es adonde queríamos llegar.
Esta conjetura se ha comprobado que se cumple para millones de billones de valores de z, para ello miles de personas ofrecieron el uso de sus ordenadores a través de internet ¿Que son los trillones comparados con el infinito?, ¿Quién asegura que en el quintillón no habrá puntos que incumplan la conjetura? ¡Así son los matemáticos de quisquillosos!
Pero, ¿por qué es este problema tan importante? La primera respuesta es porque nadie lo ha resuelto en más de siglo y medio, pero hay más razones y ahora aprovecho para sacar el conejo de la chistera.
Resulta que la función ζ(s) tiene una extraña conexión con los números primos pues se demuestra (la demostración, que es muy elegante, puede encontrarse en este enlace) que ζ(s) también puede obtenerse de la siguiente forma:
En esta función aparece el símbolo p que significa primo. Si vamos a DRAE primo tiene muchas acepciones. Por ejemplo: “Persona incauta que se deja engañar o explotar fácilmente”. Esa no nos vale, en el DRAE hemos de escribir “número primo” para obtener el sentido que aquí le damos: “El entero que solo es exactamente divisible por sí mismo y por la unidad”, pues bien esa p es la que hace realmente maravillosa a esta función.
Si escribo: 117, 119, 121, 123, es fácil adivinar que lo que sigue y lo que antecede, responde a la fórmula 2 n +1, que no es otra cosa que los números impares.
Si escribo: 37, 50, 65, 82, 101, 122, 145, 170 con un poco más de esfuerzo se ve que responde a la fórmula: n2+1.
Pero si escribo: 197, 199, 211, 223, 227, 229 la continuación es más difícil, corresponde a la sucesión de números primos y resulta que no hay ninguna fórmula que permita obtenerlos. Para obtener el siguiente debemos comprobar si el siguiente impar (el único primo par es el 2) es divisible por alguno de los anteriores primos si lo es hacemos la misma comprobación con el siguiente impar hasta llegar a uno que sea primo (hay algunos atajos, como la criba de Eratóstenes, pero eso no cambia pero la idea de lo dicho). Aparentemente los primos no siguen ninguna regla, parece como si estuviesen distribuidos al azar: a veces hay dos impares seguidos que son primos (se les llama primos gemelos) y a veces tenemos que probar muchos números antes de llegar al siguiente primo. Además, cualquier número natural se puede obtener de forma única como producto de números primos. Por tanto, a partir de los primos podemos obtener el resto de los naturales, y dividiendo números naturales obtenemos los racionales, y así podríamos continuar hasta obtener todos los números. Por eso, muchos matemáticos consideran a los primos los átomos de los números (auténticos átomos, no como los de los físicos, que son divisibles).

Ha habido numerosos intentos por encontrar una expresión matemática sencilla que permita encontrar un patrón en el orden en los primos y solo se han llegado a fórmulas aproximadas y ζ(z) nos ofrece ese patrón y como consecuencia algunos especulan que podrían romperse los códigos de encriptación, tan habituales en transacciones comerciales. Pero todo no acaba ahí, parece ser que tras algunas de las funciones utilizadas en mecánica cuántica y física del caos está la zeta de Riemann. La zeta de Riemann, como ya ha ocurrido con otros resultados de las matemáticas, se desarrolló sin fin práctico y “casualmente” una vez descubierta sirve para modelar algún fenómeno de la naturaleza ¿Estaba ya ahí y el hombre lo único que ha hecho es descubrirla? Albert Einstein decía que la casualidad es la manera que tiene dios de mantenerse en el anonimato. Quizás Dios creó los números primos y el tiempo, se tumbó a la bartola, y desde entonces su juguete se puso a trabajar y así lleva 13 800 millones de años.
Si entre whatsapp y whatsapp algún joven ha llegado hasta aquí, ya sabe que tiene un reto: resolver la hipótesis de Riemann, aunque fracase en el intento en el camino se encontrará paisajes que ni en el mejor de los sueños podría imaginar. Al respecto me viene a la memoria el anuncio de Ernest Shackleton puso en un periódico para conseguir aventureros para su expedición al Polo Sur: “Se buscan hombres para peligroso viaje. Salario reducido. Frío penetrante. Largos meses de completa oscuridad. Constante peligro. Dudoso regreso sano y salvo. En caso de éxito, honor y reconocimiento”.
Aunque fracasó la expedición, como probablemente le ocurrirá a la mayoría que intenteis resolver la hipótesis de Riemann, se considera una de las aventuras épicas más grandiosas del siglo XX.
———————-
Este artículo nos lo envía Guillermo Sánchez León, Profesor en la Universidad de Salamanca y autor de más de 100 artículos y ponencias, algunos de divulgación científica que podéis encontrar en su web. Además, y como complemento al artículo el autor detalla algunos calculos en: Una introducción a la hipotesis de Riemann con Mathematica.
Si tienes un artículo interesante y quieres que lo publiquemos en Naukas como colaborador invitado, puedes ponerte en contacto con nosotros.