
Solemos entender el mundo cómo un sistema que funciona en un sistema numérico en base 10, o decimal. El sistema métrico funciona en base 10, y usamos potencias de este número para representar números muy grandes o muy pequeños para expresar cómo una secuencia de símbolos (2,3×106 en lugar de 2.300.000) y también solemos redondear hasta cantidades dadas por el sistemas en base 10, tanto en la vida cotidiana cómo en aplicaciones técnicas.
Nuestros cerebros ya están prácticamente programados para pensar en decenas y centenas, y debido a eso, le atribuimos algún tipo de valor especial al número 10, a pesar de que es simplemente un número. La decisión de nuestros ancestros de usar un sistema en base 10 para representar los números fue casi completamente arbitraria, y no debido a alguna cualidad especial inherente que el número 10 tenga.
Hagamos una pequeña revisión de los distintos sistemas numéricos que existen hoy en día.
El sistema más usado es el sistema en base 10, ya mencionado anteriormente, pero también se usan con bastante frecuencia el sistema binario y el sistema hexadecimal. Estos dos sistemas se usan en informática y están en base 2 y 16 respectivamente. ¿Qué significa que funcionen en base 2 o 16?
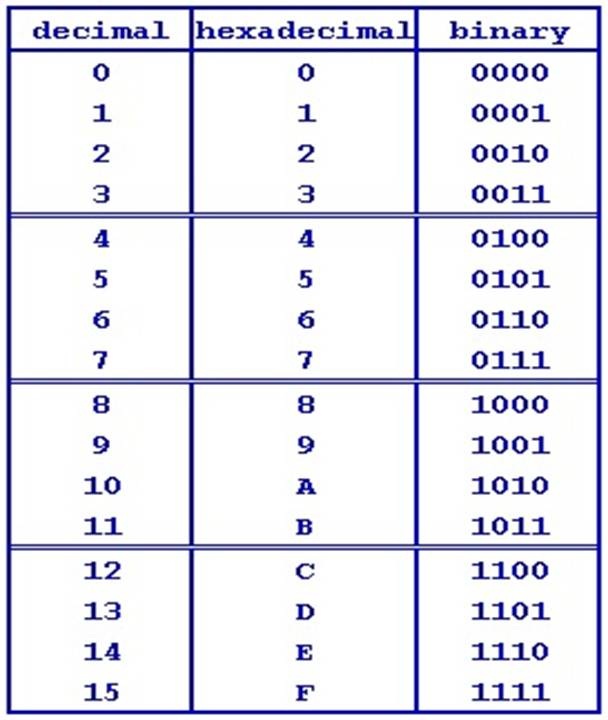
Tomemos el sistema binario cómo ejemplo. Sistema en base 2 significa en términos simples que sólo existen dos símbolos para representar todos los números (el número de símbolos no siempre es el mismo que la base del sistema numérico, pero comúnmente se da este fenómeno y facilita la explicación). En el sistema decimal hay diez símbolos, 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 que se usan para representar todos los números, mientras que en el sistema binario solo se usan los símbolos 0 y 1.
¿Cómo se hace esto? El “0” binario y decimal es el mismo, así como el “1”. Es cuando llegamos al número dos que se notan las diferencias. En sistema binario no existe el símbolo “2”, ¿Cómo lo representamos entonces? Deberíamos usar dos símbolos, el “1” y “0”. Entonces el “2” se expresa cómo “10”en binario. Listo, solucionado el problema del número dos. ¿Qué hacemos ahora con el tres? Podemos expresarlo cómo “11”, el cuatro se expresaría cómo “100”, el cinco cómo “101”, el seis cómo “110” y el siete cómo “111”. De esta forma se pueden expresar todos los números usando solamente dos símbolos.
El sistema hexadecimal en cambio tiene dieciséis símbolos, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F. La combinación de símbolos “10” en sistema hexadecimal representa el número dieciséis, mientras que la combinación “1F”, por ejemplo, representa el número treinta y uno, y “20” representa el treinta y dos.
Entonces, existen estos tres sistemas numéricos en el mundo moderno, ¿Pero qué sistemas se usaban en la antigüedad?
En muchas culturas, incluyendo chinas, griegas e hindo-árabes (sistema del cuál deriva la numeración moderna) se utilizaban sistemas en base diez. Esto es probablemente debido al hecho de que tenemos diez dedos y desarrollar un sistema numérico derivado de la forma más primitiva de contar (usando los dedos de las manos) tiene sentido. Los sistemas de contar en base veinte también fueron muy populares, siendo usado por mayas, galos, celtas y varias otras culturas. Remanentes del sistema base veinte todavía se puede observar en muchos números franceses. El numero ochenta se llama “quatre-vingt”, literalmente “cuatro-veinte”, y el noventa se llama “quatre-vingt-dix”, o “cuatro-veinte-diez”. Los sistemas de numeración en base cinco también fueron comunes, por la misma razón que los sistemas en base diez.
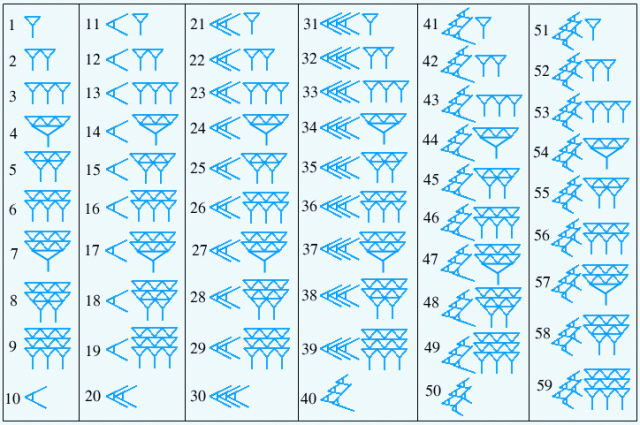
La tribu Yuki del norte de California usaba un sistema en base ocho, ya que en lugar de contar con los dedos contaban usando los espacios entre los dedos. Los antiguos sumerios desarrollaron un sistema en base sesenta, o sexagesimal. Este fue uno de los primeros sistemas numéricos desarrollados en la historia. El sistema sexagesimal nos dejó como legado el sistema de segundos, minutos y horas, que funcionan en base sesenta.
Existe también un caso notable en que inexplicablemente se usa un sistema en base veintisiete, y se trata del lenguaje de los Telefol, habitantes de Papua Nueva Guinea.
Existe sin embargo un cuarto sistema en el mundo moderno (y antiguo) que subrepticiamente se sigue usando por casi todo el mundo, en la mayoría de las culturas. Se trata del sistema en base doce, o duodecimal (docenal para los puristas). En el comercio y la vida cotidiana es muy común usar docenas en lugar de decenas, y gruesas en lugar de centenas. Esto se debe a que el doce tiene más factores que el número diez. El diez se puede dividir por 1, 2, 5 y 10, mientras que el doce se puede dividir en 1, 2, 3, 4, 6 y 12. Al tener más factores, se puede dividir con mucha más facilidad. Es fácil dividir una doce de huevos en tres, o cuatro, o dos, mientras que dividir una decena de huevos en tres es imposible sin romper un huevo. Es por el pragmatismo del sistema duodecimal que se ha usado en el comercio a través de la historia, independientemente del sistema numérico que se use para contar.
El número doce también se usa para contar los meses, ya que se hace muy fácil dividir el años en cuatro (cuatro estaciones o trimestres), dos (dos semestres), seis (seis bimestres), etc. Entonces se hace evidente que el número doce es más práctico que el número diez. Es quizás por esto mismo que el número doce ha tenido un significado especial en la mayoría de las culturas a través de la historia; doce tribus de Israel, doce apóstoles, doce signos del zodiaco, doce signos zodiacales chinos, las doce labores de Hércules, los doce hijos de Odín, etc.
Los modernos proponedores de un cambio por el sistema docenal suelen usar doce símbolos para contar, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, un “2” invertido para representar el diez y un “3” invertido para representar el once.
La anatomía de nuestras manos también nos permite contar usando un sistema en base doce, si utilizamos un poco nuestra imaginación. Se puede contar tocando cada falange de los dedos con el pulgar, permitiéndonos llegar hasta doce con una sola mano. Con la segunda mano podemos contar las docenas, por lo que se puede contar hasta ciento cuarenta y cuatro usando un sistema en base doce. Nada mal, ¿o no?

No pretendo convencer a los lectores sobre la superioridad del sistema duodecimal, pero es notable darse cuenta de cuán condicionados y programados estamos para ver el mundo de cierta forma. El número diez no tiene ninguna propiedad especial, y sin embargo estamos entrenados desde pequeños para entender el mundo desde ese sistema. La cultura en la que estamos insertos afecta muy poderosamente (e invisiblemente) la forma en que interpretamos y observamos el universo y los fenómenos naturales. Creo que la lección es que a veces no hace daño desaprender algo para poder aprender cosas nuevas.
Este artículo nos lo envía Vicente Muñoz Walther. Ingeniero en Biotecnología Molecular de la Universidad de Chile, en Santiago de Chile. En la actualidad trabaja en el laboratorio de Virología Molecular de la Fundación Ciencia & Vida. Vicente también escribe cuentos cortos de fantasía y ciencia ficción, los cuáles podéis leer en cuentosdeltente.blogspot.com.
Referencias y más información:
Ascher, Marcia (1994), Ethnomathematics: A Multicultural View of Mathematical Ideas, Chapman & Hall
Telefol at Ethnologue (18th ed,. 2015)
Ifrah, Georges (2000) The Universal History of Numbers: From prehistory to the invention of the computer, John Wiley and Sons.
Si tienes un artículo interesante y quieres que lo publiquemos en Naukas como colaborador invitado, puedes ponerte en contacto con nosotros.
