
Los registros de escritura más antiguos que poseemos provienen de la civilización babilónica en el cuarto milenio antes de nuestra era, y por supuesto entre el tesoro de las miles de tabletas de arcilla que hemos descubierto, no pueden faltar las matemáticas. Se puede decir que el lenguaje matemático tuvo ascendencia en las civilizaciones más tempranas, prácticamente al mismo tiempo, o aún antes, del lenguaje escrito: hay registros de antiguos métodos de contabilizar por medio de nudos hechos en cuerdas en civilizaciones asiáticas que predatan sus escrituras.
Los babilonios desarrollaron la maravillosa escritura cuneiforme y el también maravilloso sistema de escritura en tabletas de arcilla que ha resistido el paso de los milenios, a diferencia de nuestros modernos sistemas para almacenar información, que son tan frágiles que es posible que grandes cantidades de información de nuestra época estén en peligro de perderse. Gracias a este tesoro del pasado que hemos podido encontrar y descifrar, podemos ver que el pensamiento humano, una vez entrado en la etapa avanzada de desarrollo de lenguaje y de escritura, ha sido pronto no sólo para realizar cálculos básicos de ovejas y ladrillos, sino de lograr abstracciones mentales sofisticadas y más aún: divertirse y retarse con ellas.
Si bien los matemáticos babilonios tenían las asignaciones básicas de contabilizar, administrar y repartir, muy pronto encontraron en sus estudios áreas más allá de la mera practicidad diaria. En la geometría y la aritmética desarrollaron métodos sofisticados de cómputo: por ejemplo la imagen principal de este artículo, la tableta conocida como Plimpton 322, es una tabla de triples pitagóricos: el llamado “Teorema de Pitágoras” era bien conocido para ellos, un milenio antes de que el famoso griego lo formalizara.
Los matemáticos de Mesopotamia también podían resolver problemas con incógnitas: esto es que en términos modernos, sabían de álgebra. De hecho, se han descubierto cientos de tabletas con ejercicios que podríamos llamar “inútiles”: problemas cuyo único fin era entrenar al escriba en la resolución de problemas, expuestos de formas que nunca se podrían encontrar en el mundo real.
Ahora bien, leyendo las descripciones de estos problemas también podemos obtener una deliciosa sensación de “otredad”, de ver una cultura totalmente diferente que se plantea las cosas desde una perspectiva muy singular. Si pensamos que las matemáticas son un lenguaje universal y sin ambigüedades, esto no quita que al ver un problema babilonio nos topemos de entrada con un planteamiento al que no estamos acostumbrados en absoluto.
Pongo por ejemplo uno de estos problemas, encontrado en la tableta YBC4652 (por las siglas del Yale Babylonian Catalogue), mejor conocida como “La Tableta de Pesar Piedras”. Esta es la tableta, con su re-escritura a la derecha:
 La traducción literal ya nos da una probada de un problema que parece que empezamos a entender pero que a la mitad, nos deja estupefactos:
La traducción literal ya nos da una probada de un problema que parece que empezamos a entender pero que a la mitad, nos deja estupefactos:
Encontré una piedra, pero no la pesé.
Tomé 8 veces su peso y agregué 3 gin.
Tomé un tercio de un treceavo y lo multipliqué por 21,
lo sumé y lo medí:
encontré que era igual a un ma-na.
¿Cuánto pesaba la piedra?
La piedra pesaba 4 gin y medio.
Nos perdemos totalmente en la línea 4. ¿“Pesé y medí” qué? La tableta no incluye más información, pero un escriba no hubiera encontrado dificultad alguna para entender el problema. El sentido completo de éste se completa cuando vemos lo que aquellos matemáticos sobreentendían. Aquí está el planteamiento completo, con la información extra en paréntesis:
Encontré una piedra, pero no la pesé.
Tomé 8 veces su peso y agregué 3 gin
(esto me da una cantidad original).
Tomé un tercio de un treceavo y lo multipliqué por 21,
(y al multiplicarlo por la cantidad original, obtuve una segunda cantidad).
(Luego, sumé la cantidad original con la cantidad nueva).
Al ver la suma,
encontré que era igual a un ma-na.
¿Cuánto pesaba la piedra?
La piedra pesaba 4 gin y medio.
Ohhh. OK. Pues sin eso, nunca hubiéramos sabido. Los traductores que han realizado estas labores han tenido que ver cientos de este tipo de problemas para poder entender la forma en que los ejercicios eran propuestos, pero han tenido además la suerte de que la mayor parte de las respuestas se proporcionan ahí mismo, de modo que han podido calcular para comprobar la certeza de sus traducciones.
Ahora bien, para mi lector con inclinaciones matemáticas, el problema es éste: dado que las unidades de peso mencionadas tienen la siguiente equivalencia:
1 ma-na = 60 gin,
¿Cuál es la formulación correcta del problema, usando nuestra notación algebraica moderna? Esto es, ¿cómo construir una ecuación con una incógnita x para resolverlo?
La respuesta al final de este artículo.
Referencias:
Internet history is fragile. This archive is making sure it doesn’t disappear. PBS NewsHour. Enero 2, 2017.
Fauvel, John y Gray, Jeremy, eds., The History of Mathematics: A Reader. Basingstoke: Macmillan/Open University, 1987. 1.E. 1 (20).
Eleanor Robson. Babylonian Maths. University of Cambridge. 2008.
*
*
*
*
Solución:
Tenemos una piedra de peso desconocido, este peso es nuestra x, que expresaremos en la unidad llamada gin. Este peso, lo multiplicamos por 8 y le añadimos 3: tenemos así la expresión 8x + 3. Ésta es la “cantidad original”. Después, esta cantidad tenemos que multiplicarla por el extraño “un tercio de un treceavo, por 21”: lo que quiere decir que primero tomamos (1/3) x (1/13) x 21, o sea (21/39), y tomamos esto para multiplicarlo por la cantidad original (8x + 3), dándonos la “cantidad nueva”. Finalmente sumamos ambas cantidades y obtenemos la medida de 1 ma-na, que expresaremos como 60 gin para poder tener la ecuación con un solo tipo de unidad:
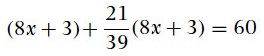
Nací en México y vivo en China desde el 2000, donde estudié idioma e historia, y luego fui investigador visitante en el Centro Internacional Wan Lin Jiang de Economía y Finanzas, así como profesor de economía e historia para extranjeros en la Universidad de Zhejiang. Actualmente dirijo el Mexico-China Center y doy conferencias acerca de ciencia y cooperación tecnológica internacional.
