No, no es un post sobre bondage, pero quédate, igual te gusta más… o te deja más secuelas.
Imagina que te digo que elijas dos números. Puedes escoger uno y luego el otro, tienes dos grados de libertad.
¿Y si te digo que elijas dos números, pero que su suma sea 7? Ahora puedes escoger libremente el primero, pero no el segundo. Eso es porque ahora tienes dos variables y una ligadura, lo que te deja sólo con un grado de libertad.
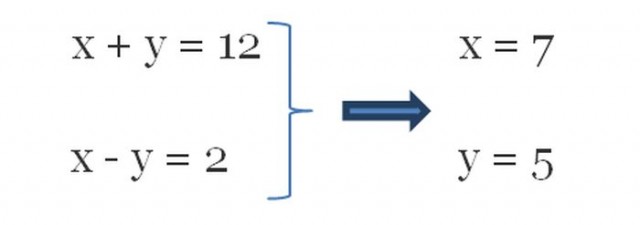
Imagina ahora que te propongo que elijas dos números cuya suma sea 12 y cuya diferencia sea 2. En este caso, no tienes libertad para escogerlos, lo que sí puedes hacer es resolver el sistema de ecuaciones (así lo llamamos), porque sólo hay dos números que cumplan esas dos condiciones.
¿Qué ocurriría si impongo más ligaduras que variables?
Pues, o bien las nuevas ligaduras en realidad son una combinación de las antiguas (como en nuestro caso exigir que el producto de los dos números de 35), o bien resultaría imposible encontrar una solución al problema (por ejemplo si exigiéramos también que los números sumasen 45).
También puede ocurrir que con sólo dos ligaduras el problema no tuviera solución, si las ligaduras estuvieran suficientemente “mal puestas”. Por ejemplo, escoge dos números que sumen 12 y, a la vez, que sumen 13.
Y, también puede suceder que esas dos ligaduras fueran en el fondo la misma, o que no tuvieran “fuerza” suficiente para fijar las variables. Por ejemplo, dos números que sumen 5 y que multiplicados por dos, sumen diez (estas dos exigencias, de hecho, son la misma).
Dejamos aquí esto un momento.
Seguro que conocéis la palabra teorema (según el DRAE: Proposición demostrable lógicamente partiendo de axiomas o de otros teoremas ya demostrados, mediante reglas de inferencia aceptadas.)
Dicho más sencillito (quizá menos preciso): Conclusión lógica a partir de ciertos principios.
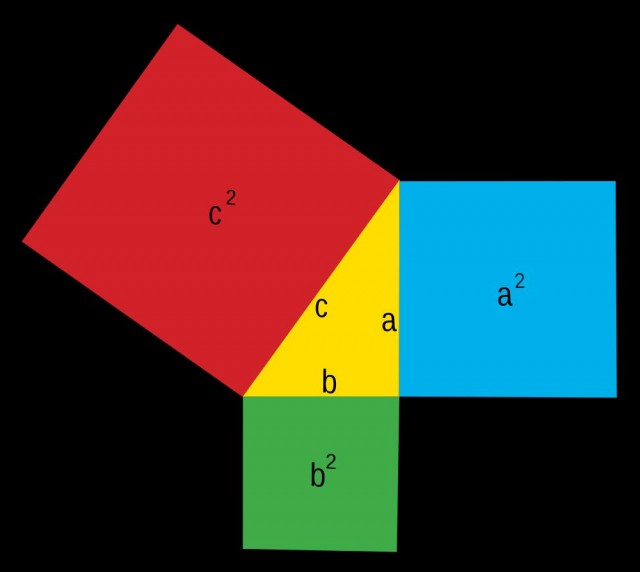
Todos habréis oído hablar del Teorema de Pitágoras. Aquello de que la suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa en un triángulo rectángulo.
Esto puede demostrarse usando los axiomas de la geometría. Dicho de otro modo, este resultado está implícito en los axiomas. Nosotros simplemente, nos vamos dando cuenta de esas implicaciones lógicas que estaban ocultas en los axiomas que aceptamos.
Es como si alguien te dice: “Cierra por fuera”. Como teorema podemos deducir que debes salir de la habitación.
Y ahora, vamos con la segunda parte del título “de hombres”.
Hay personas que depositan su lealtad en distintos “lugares”: su pareja, sus hijos, su familia, su religión, su patria, la verdad, distintas filosofías, el dinero, el puro bien físico personal, etc.
Podíamos usar el principio de este post para hacer una metáfora. Yo tengo cierta libertad de acción, pero acepto “ligaduras”, depositando mi lealtad en cualquiera de esas cosas que decíamos hace un momento.
Y aquí es donde quería poner yo el acento: ¿Qué ocurre si tus “ligaduras” (tus lealtades) son incompatibles? No puedes servir siempre a tu patria y a la verdad, porque llegará un momento en el que el interés patrio pase por no revelar ciertas cosas.
O, ¿qué ocurre si de tus lealtades (de tus principios o axiomas) se derivan teoremas que iban implícitos en ellos y en los que no habías reparado? Por ejemplo, la adhesión inquebrantable a ciertos preceptos religiosos (como ocurre con las transfusiones de sangre y los testigos de Jehová) podría llevarte a poner en riesgo la salud o la vida de tus hijos, cosa que nos repugna y con la que quizá no contábamos al aceptar esa fe.
Ayer recordaba aquella frase que le decían al Cid “Dios, qué buen vasallo si tuviera buen señor.” Nosotros elegimos dónde vamos a depositar nuestra lealtad y por muy coherentes e íntegros que seamos al seguir nuestros principios, si estos no son buenos (no son un buen señor), nuestro comportamiento no será beneficioso para nosotros ni para nuestro entorno.
Aquí también me venían a la memoria las leyes de la Robótica que ideó Isaac Asimov pensando en que deberían ser incluidas en la programación de cualquier robot que tuviera un comportamiento autónomo… para protegernos a las personas.
Por si alguien no las conoce son:
- Un robot no debe dañar a un humano o permitir que sufra daño (Ser buenos)
- Un robot debe obedecer las órdenes de un humano (Ser obedientes)
- Un robot debe protegerse a sí mismo (No ser imbécil e ir dándose cabezazos…)
Cualquiera que haya leído sobre drones, sabrá que hoy no hacemos ni caso de estas leyes y usamos robots matar gente (aunque nuestros robots no sean autónomos).
Pero a lo que iba, ¿veis que es imposible ser completamente fiel a estos tres “axiomas” a la vez? Hay conflicto si ordenamos a un robot que mate a alguien… cuando salvar a un humano pone en riesgo a un robot…
La manera de solucionar esto es establecer una jerarquía. La primera ley es más fuerte que la segunda y la segunda más que la tercera. Así que un robot obedecerá si no pone en peligro a humanos y se protegerá a sí mismo si no pone en peligro a humanos y si con eso no desobedece ninguna orden.
Concluyendo, y agradeciendo que leáis mis desvaríos, es de extremada importancia dedicar un momento a ver dónde hemos puesto nuestra lealtad, si hay algún tipo de jerarquía entre ellas, qué cosas implican esas lealtades y a qué lugares nos pueden llevar.
De otra forma te puedes encontrar confuso en tu intento de llevar una vida íntegra haciendo cosas como
– No contarle a nadie que tu pareja te está haciendo daño por respetar la intimidad de la pareja
– No denunciar delitos que se cometen en tu trabajo por lealtad a tu empresa
– Llevar a cabo actos con los que no estás de acuerdo moralmente por cumplir con la palabra dada
– Mentir a personas inocentes y que eso les perjudique por proteger un secreto que te has comprometido guardar
– Hacer lo que consideras incorrecto moralmente porque es legal, o bien…
– Dejar de hacer lo que consideras correcto moralmente porque no se ajusta a la ley
Y una larga lista que podéis aumentar en los comentarios…
Este post está dedicado a los chavales de Brunete que junto a Bárbara se pasan por mi blog, a ver qué cosas “me se ocurren”. Espero que os dé un punto de partida para hablar de mates, de robótica y, sobre todo, de vosotros mismos.
He aprendido un par de cosas y me encanta contarlas… Estudié Física y un DEA en Telecomunicaciones. Trabajo de profe de instituto enseñando Tecnología. Escribo libros de divulgación, ya voy por el quinto, y desde hace unos años llevo también el blog La Ciencia para todos. Salgo de vez en cuando por la tele o la radio y voy de pueblo en pueblo haciendo mis cacharritos… En fin, que si encuentro una oreja dispuesta y unos ojillos brillantes, me encanta transmitir la Belleza que yo encontré en la Ciencia.