Recientemente hemos sabido que el paro registrado en España se ha reducido en algo más de 250.000 personas respecto a las mismas fechas del pasado año. Si bien el dato es positivo, hay un asunto tras todo esto que lleva tiempo escamándome, y que ya he visto en multitud de casos: la manía de centrar la atención en la variable incorrecta.
Me explicaré. Cuando uno pretende hacer un análisis cuantitativo de cualquier sistema complejo, es de vital importancia escoger qué variable o variables deben observarse de modo que arrojen la mayor cantidad de información posible… y un incremento nunca es una buena variable, puesto que siempre destruye información.
Más en detalle, estas son las dos características más indeseables de los incrementos:
- No dicen nada sobre los valores totales. Si yo subo el escalón de mi portal, y tú subes el último escalón del Empire State Building, ambos hemos incrementado nuestra altura en un escalón.
- Los incrementos se calculan en intervalos (incremento mensual, anual, etcétera), y dichos intervalos son arbitrarios. Existe una salvedad interesante: cuando el intervalo se hace tender a cero, cosa no siempre posible, y que da lugar al concepto matemático de derivada.
Veamos un ejemplo:
Imagine el lector que tiene la capacidad de comprar una empresa. Hay dos empresas interesantes, la empresa A lleva tres años aumentando sus ingresos a razón de 10.000 € más cada año, y la empresa B, en cambio, lleva tres años ganando 20.000 € menos al final cada ejercicio.
Jugando con este modelo tan simplificado, ¿cuál de las dos empresas sería una mejor compra?, pudiera parecer que la empresa A es más prometedora, pero la única respuesta razonable es que faltan datos para saberlo.
Unos datos netos compatibles con lo anterior podrían ser los siguientes:
Quedando claro, viendo los datos netos, que la empresa B es una apuesta mucho mejor. Y lo que es más importante, los incrementos también están ahí. El paso de datos netos a incrementos puede hacerse sin dificultad, pero el paso inverso no es posible en general.
Por cierto, en matemáticas esta es la causa de que las integrales indefinidas (operación inversa a la derivada), siempre se incluya la famosa constante (+ c), que da cuenta de esta imposibilidad de invertir de forma unívoca. En el siguiente gráfico podemos ver cómo el paso de valores netos a derivada puede hacerse de forma unívoca:
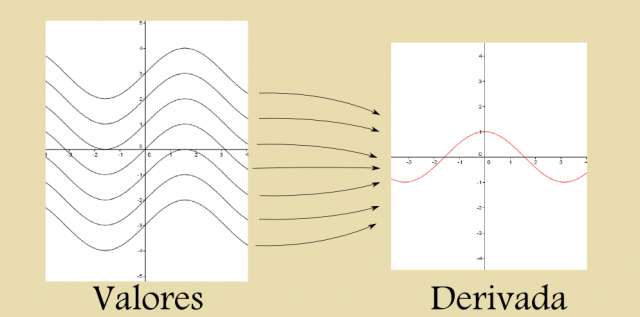
Sin embargo, en el paso inverso (conocida la derivada, hallar «la» función compatible con dicha derivada), tenemos infinidad de opciones disponibles.

En resumen: desconfiad siempre los incrementos.
Nota: en el caso concreto de los datos del paro, que ha servido como ejemplo en este artículo, cabría discutir además si los valores netos del número de parados son la variable más adecuada o si sería más apropiado utilizar, por ejemplo, el número de afiliados a la seguridad social, o quizá algo más creativo cómo el número de horas de trabajo. Pero en este artículo he querido centrarme solamente en lo poco recomendable de usar los incrementos.
Pablo Rodríguez (Guadalajara, España, 1984) se siente inclinado de un modo casi suicida hacia las cosas complicadas. Esta cualidad le ha llevado a convertirse en físico, malabarista, ilusionista aficionado y humorista de cuarta categoría. Actualmente trabaja como experto en computación científica en el Netherlands eScience Center. Más información aquí

