Algunas propiedades del Conjunto de Cantor

Cuando alguien nos habla de conjuntos fractales, se pone a pensar en esos dibujos cuasi-artísticos llenos de autosemejanzas y formas que se asemejan a árboles, rayos, nubes… No andamos desencaminados, pues la principal característica de un fractal es precisamente ésa, la autosemejanza. Sin embargo, hay conjuntos de este tipo extremadamente sencillos: tan sencillos que caben en un simple intervalo. Hoy vamos a ver algunas de las propiedades más sencillas de explicar y curiosas de, quizás, el primer fractal conocido: El Conjunto de Cantor.

¿Cómo se construye?

Antes de empezar, y como buenos matemáticos que somos, vamos a definir rigurosamente el objeto con el que vamos a trabajar. El Conjunto de Cantor se construye por un proceso de paso al límite por iteración: veamos cómo.

Partamos del intervalo unidad $I_0=[0,1]$ , es decir, nuestro estado inicial es el intervalo cerrado de extremos $0$ y $1$ , cuya longitud es exactamente $1$ .

Seguidamente, partimos este intervalo, $C$ , en 3 partes idénticas y eliminamos el interior (conservando siempre los extremos). Así llegamos a nuestra primera iteración, que será $I_1:=[0,1/3]\cup[2/3,1]$ , es decir, $I_1$ es la unión de 2 intervalos cerrados (y disjuntos) cada uno de ellos de longitud 1/3. Si queremos, podemos llamar $C_0=[0,1/3]$ y $C_,1=[2/3,1]$ .

Prosigamos. Repetimos el proceso anterior a cada uno de los intervalos $C_0$ y $C_1$ , es decir, los dividimos en 3 partes iguales y eliminamos las centrales (conservando los extremos). Así, en la segunda iteración, llegamos al conjunto $I_2=[0,1/9]\cup[2/9,1/3]\cup[2/3,7/9]\cup[8/9,1]$ , es decir, la unión de 4 intervalos cerrados disjuntos cada uno de ellos de longitud 1/9. Como antes, podemos ponerles nombres; así, $C_{0,0}=[0,1/9]$ , $C_{0,1}=[2/9,1/3]$ , $C_{1,0}=[2/3,7/9]$ y $C_{1,1}=[8/9,1]$ . Fijaos que los intervalos $C_{0,x}$ proceden de la división de $C_0$ mientras que los de la forma $C_{1,x}$ proceden de $C_1$ .

Por si aún no se ven las cosas claras, hagamos una tercera iteración y dividamos cada uno de los 4 intervalos anteriores en 3 partes iguales, quitemos las centrales y quedémonos con los extremos. Llegamos al siguiente conjunto:

$\displaystyle I_3=[0,1/27]\cup[2/27,1/9] \cup [2/9,7/27]\cup[8/27,1/3]\, \cup\,$ $\displaystyle [2/3,19/27]\cup[20/27,7/9] \cup [8/9,25/27]\cup[26/27,1]$

es decir, la unión de 8 intervalos disjuntos de longitud 1/27, a los que llamaremos, siguiendo la notación anterior, $C_{0,0,0},\,C_{0,0,1},\,C_{0,1,0},\,C_{0,1,1},\,C_{1,0,0},\,C_{1,0,1},\,C_{1,1,0},\,C_{1,1,1}$ .

Venga, veamos un dibujo de cómo va quedando todo esto:

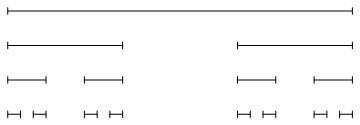
Primeras iteraciones del Conjunto de Cantor

Bien, y ahora… ¿cual es el Conjunto de Cantor? Pues muy sencillo, el Conjunto de Cantor como la intersección de todas las iteraciones anteriores (las 3 que hemos visto y las sucesivas que hagamos), es decir, $\displaystyle C=\bigcap_{n=1}^{\infty}I_n$ .

¿Y no hay una forma más fácil de definirlo?

Más fácil no lo sé… pero sí que hay otra. Si nos fijamos bien, eso de quitar el intervalo del centro en cada iteración nos dice que los puntos del Conjunto de Cantor, si los expresamos en base 3 (con decimales, vamos) no contienen el 1.

¿Cómo? ¿que no contienen el 1? Pues no. ¿Y $1/3$ éste número sí está en el Cantor, pero su expresión decimal en base 3 es $0,1$ . Ya, querido lector… pero también recuerda que en base 3, $0,1=0,0222\dots$ y esta expresión ya no contiene el 1. Así, podemos decir, sin lugar a equivocarnos, que el Conjunto de Cantor es el conjunto de los puntos de $[0,1]$ que pueden escribirse en base 3 sin contener al 1, es decir

$\displaystyle C=\left\{x\in[0,1]:\ x=\sum_{n=1}^{\infty}\frac{a_n}{3^n},\, \text{ donde }a_n=0,2,\,\forall n\in\Bbb{N}\right\}$

¿Cuánto mide?

Si nos fijamos, en cada paso que damos para acercarnos al verdadero conjunto de Cantor, partimos de 1 intervalo de longitud1, después llegamos a 2 intervalos de longitud $1/3$ , 4 de longitud $1/9$ , 8 de longitud $1/27$ …. y en el enésimo paso tendremos $2^n$ intervalos de longitud $1/3^n$ , es decir, cada iteración tendrá una longitud de $l_n=long(I_n)=2^n\cdot (1/3^n)=(2/3)^n$ . Por lo tanto, la longitud del Conjunto de Cantor sería el límite de estas longitudes, es decir

$\displaystyle long(C)=\lim_{n\to\infty}l_n=\lim_{n\to\infty}(2/3)^n=0$

Es decir, el conjunto de Cantor mide $0$ (Si quieres saber algo más de la longitud o medida de Lebesgue en $\Bbb{R}$ puedes mirar la construcción de un conjunto que no se puede medir).

Por si no te convence, vamos a verlo de otra forma. Calculemos la longitud de los trozos que quitamos. En la primera iteración quitamos $1=2^0$ segmento de longitud $1/3=1/3^1$ ; en la segunda $2=2^1$ segmentos de longitud $1/9=1/3^2$ ; en la tercera $4=2^2$ segmentos de longitud $1/27=1/3^3$ ; y así sucesivamente, en la enésima iteración habremos eliminado, además de todo lo anterior, $2^{n-1}$ segmentos de longitud $1/3^n$ cada uno.

En total habremos quitado del intervalo $[0,1]$ original (cuya longitud es obviamente 1) la siguiente cantidad

$\displaystyle\sum_{n=1}^\infty 2^{n-1}\cdot\frac{1}{3^n}=\frac{1}{2}\sum_{n=1}^\infty \left(\frac{2}{3}\right)^n= \frac{1}{2}\cdot \frac{2/3}{1-2/3}=1$

Luego la longitud del conjunto de Cantor será $1$ (la del intervalo $[0,1]$ ) menos la que nos acaba de salir (otra vez 1)… $0$ .

¿Cuántos puntos tiene?

Bien, ya sabemos que el Conjunto de Cantor tiene longitud $0$ , como un único punto, o como una cantidad finita de puntos…. incluso igual que una cantidad numerable de puntos. Así que nos podemos preguntar… ¿cuántos puntos hay en el Conjunto de Cantor? Porque si resulta que este conjunto es numerable, el que tenga longitud $0$ no nos dice nada (se trata de una propiedad intrínseca de la longitud o, mejor dicho, de la medida de Lebesgue).

Por un lado, como el Conjunto de Cantor está contenido en el intervalo $[0,1]$ , tendrá tantos puntos o menos que éste. Vamos a comprobar que, en realidad, ambos tienen la misma cantidad de puntos, y para ello, vamos a construir una sobreyección de $C$ en $[0,1]$ , es decir, a cada punto de $C$ le vamos a asociar otro punto de $[0,1]$ de forma que abarquemos todos, pero, quizás, haya puntos que procedan de más de uno del conjunto de Cantor. Vamos allá.

¿Os habéis fijado en la forma tan particular que hemos elegido para denotar los subconjuntos de $C$ ? Esa es la clave. Seleccionemos un punto del conjunto de Cantor. La construcción de $C$ me dice que este punto estará (de hecho él mismo será) en la intersección de una sucesión de intervalos de los pasos intermedios: un intervalo por cada paso. Así, nuestro punto estará bien en $C_0$ bien en $C_1$ (pongamos el primero); en la segunda etapa, estará bien en $C_{0,0}$ bien en $C_{0,1}$ (pongamos el segundo); en la tercera estará en $C_{0,1,0}$ bien en $C_{0,1,1}$ y así sucesivamente. Si os fijáis, lo que hacemos es que en cada etapa, elegimos un número: el 0 ó el 1, por lo que al final, tendremos una sucesión de Ceros y Unos que nuestro punto determina de forma única. Y aquí viene lo bueno. A nuestro punto del conjunto de Cantor, le hacemos corresponder el número decimal binario $0,0101101\dots$ . Es decir, $0,xxx$ donde $xxx$ es precisamente la sucesión de Ceros y Unos que hemos determinado.

Si nos fijamos bien, esta asignación es una sobreyección. Si fijo cualquier punto del intervalo $[0,1]$ siempre lo podré expresar como decimal binario (recordad, chicos, $0,1111\dots=1$ y $0=0,000\dots$ ). Además, esta correspondencia no es inyectiva, pues a varios puntos del conjunto de Cantor le corresponde el mismo punto de $[0,1]$ (claro, porque $0,1=0,1000\dots=0,0111\dots$ ). Total, que se podría decir que en el conjunto de Cantor hay tantos o más puntos que en $[0,1]$ , pero como antes vimos que en realidad eran tantos o menos… se deduce que en realidad tenemos la misma cantidad de puntos.

Esta demostración es muy chula (la verdad, se me ocurrió a mí solito y luego vi que el mismo argumento estaba ya escrito en muchísimos sitios), pero no es la original exactamente. La prueba original es la del método diagonal de Cantor. En él, supone que hay una cantidad numerable de puntos (vale, ya sabemos que no hay un número finito) y los ordena uno debajo de otro… escritos en forma decimal base 3 (recordad que el conjunto de Cantor se corresponde con los puntos de $[0,1]$ que se pueden expresar en forma decimal ternaria sin contener el 1). Ahora elije otro punto diferente a todos ellos y que siga estando en el conjunto de Cantor (con la propiedad esa del 1) del siguiente modo. Se fija en el primer punto y en el primer decimal, si es un 0, él elije 2 para su nuevo número, y si pone 2, elije 0. Ahora se fija en el segundo punto y en su segundo decimal… y elije para el suyo el contrario: y lo mismo para el tercer punto y tercer decimal y, sucesivamente, para el enésimo punto y su enésimo decimal: elije el contrario del que se encuentra. De esta forma, su punto es distinto a todos pero sigue teniendo la propiedad de que es expresable en forma decimal ternaria sin usar el 1, luego está en el conjunto de Cantor. Conclusión, no puede ser numerable.

¿Pero cual es entonces su dimensión?

Puf, pues sí que es raro este conjuntito. ¿Eso crees? Pues aún no has visto todo. Ya sabemos que este conjunto tiene longitud 0, pero tiene tantos puntos como el propio intervalo $[0,1]$ . Eso nos debe inducir a pensar que, quizás, la longitud no sea la forma adecuada de medir este conjunto; dicho de otro modo, a lo mejor, este conjunto NO tiene dimensión 1, sino otra algo más pequeña.

Una forma de verlo es tratar de encontrar su dimensión fractal. Nosotros estamos acostumbrados a trabajar con la dimensión topológica de un objeto (concepto introducido por Henri Poncaré), que se define como el número de variables independientes (parámetros, incógnitas…) que se precisan para describir un entorno de cada punto del objeto (es decir, me fijo en un punto del objeto y los que están muy cerca, y trato de describirlo mediante ecuaciones: el número de variables que necesite –eliminando las superfluas- es la dimensión topológica). Pero esta dimensión no es capaz de detectar las irregularidades de los objetos, como las del Conjunto de Cantor.

Así pues, se hace necesario introducir un nuevo concepto que mida, de alguna forma, la autosimilitud de los objetos. Veamos algunos ejemplos sencillos. Si tengo un segmento de longitud 1, y pretendo cubrirlo con copias suyas de tamaño $l$ , necesitaré exactamente $N(l)=1/l$ copias, es decir, $N(l)\cdot l^1=1$ ; si tengo un cuadrado de área 1 y pretendo cubrirlo con cuadraditos de lado $l$ , necesitaré $N(l)=1/l^2$ cuadraditos, es decir, $N(l)\cdot l^2=1$ ; y lo mismo si parto de un cubo de volumen $l$ , necesitaré $N(l)=1/l^3$ cubitos de lado $l$ , o lo que es lo mismo, $N(l)\cdot l^3=1$ . Si nos fijamos, la dimensión del objeto es el exponente de $l$ . Así, podemos introducir la siguiente definición:

Un objeto tiene dimensión $d$ cuando $N(l)\cdot l^d=1$ siendo $N(l)$ el número de objetos de tamaño $l$ que se necesitan para cubrir el objeto. O dicho de otro modo, la dimensión será $d=\frac{\ln(N(l))}{\ln(1/l)}$ .

Para los estrictos, la dimensión fractal de un objeto que se encuentra en el espacio $\Bbb{R}^n$ es $d$ si $\lim_{l\to0} \frac{N(l)}{1/l^d}=cte.$ , donde $N(l)$ representa, formalmente, el menor número de cubos $n$ -dimensionales de lado $l$ que se necesitan para cubrir completamente el objeto.

Bueno, vamos a trabajar con la definición sencilla y no con la formal. Si parto del conjunto de Cantor, se necesitan 2 copias de tamaño 1/3 para cubrir el conjunto de Cantor; se necesitan $4=2^2$ copias de tamaño $1/3^2$ para cubrirlo; $8=2^3$ copias de tamaño $1/3^3$ ; y así sucesivamente, se necesitan $2^k$ copias de tamaño $1/3^k$ para cubrir el Conjunto de Cantor.

Así tomando como $l=1/3^k$ ( $k=1,2,3,\cdots$ ) se necesitarán $N(l)=2^k$ copias. Así la dimensión del Conjunto de Cantor será $d=\frac{\log(2^k)}{\log(1/(1/3^k))}=\frac{\ln2}{\ln3}\approx 0.631$ .

Pero…¿cuánto mide realmente?

Y ¿esto qué significa? pues que aunque el Conjunto de Cantor se construya en $\Bbb{R}$ , la mejor forma de medirlo no es usando la longitud, es decir, la medida estándar de $\Bbb{R}$ , sino que habría que usar la medida estándar de $\Bbb{R}^{{\ln2}/{\ ln3}}$ . El problema es que esta medida es complicada de establecer. La mejor forma de hacerlo se debe a Felix Hausdorff, quien introdujo lo que hoy se conoce como medidas de Hausdorff. Básicamente, estas medidas comparan un conjunto de $\Bbb{R}^n$ con diámetros de conjuntos muy pequeños… elevados a un número $d\ge 0$ : esta sería la medida $d$ -dimensional de Hausdorff ó $H_d$ . Así, para cada número positivo $d$ , tendremos una medida. La propiedad fundamental es que si fijo un conjunto cualquiera $A\subset\Bbb{R}^n$ , se cumple que existe un número $D\ge0$ tal que $H_d(A)=+\infty$ si $d<D$ y $H_d(A)=0$ si $d>D$ . Mejor fíjate en el siguiente dibujo:

Dimensión de Hausdorff de un conjunto cualquiera

De esta forma $D$ será la verdadera dimensión de nuestro conjunto y en esta dimensión (que en el caso del conjunto de Cantor es $D=\ln2/\ln3$ ), nuetsro conjunto puede medir lo que sea entre $0$ y $+\infty$ .

Pues bien, el Conjuto de Cantor cumple que $H_{\ln2/\ln3}(C)=1$ , es decir, que en su verdadera dimensión, mide 1. Vamos, que sería el equivalente al intervalo $[0,1]$ para $\Bbb{R}$ o el cuadrado unidad para $\Bbb{R}^2$ .

¿Y no hay niguna sorpresita más?

Pues aquí no acaba la cosa. El Conjunto de Cantor no sólo presenta estas sencillas (de contar) propiedades que os hemos presentado, sino que hay muchas más: Es compacto (al ser cerrado y acotado); no posee puntos aislados, es decir, a cualquier punto del Conjunto de Cantor nos podemos acercar a través de puntos del propio Conjunto de Cantor; su interior es vacío, es decir, no contiene a ningún intervalo por pequeño éste sea (esto significa que es un conjunto disperso en $[0,1]$ ); además, no sólo no es conexo, sino que es totalmente disconexo (vamos que los puntos no se conectan ni con enchufes); y así un largo etcétera de propiedades matemáticas muy interesantes.

Pero no me gustaría terminar sin volver a sorprenderos. Con todo lo que hemos dicho, parece que el Conjunto de Cantor es muy pequeño, que es muy poquita cosa. Pero, ¿qué pasa si sumamos dos Conjuntos de Cantor? En concreto ¿qué conjunto es $C+C$ ?

Antes hay que recordar qué entendemos por suma de dos conjuntos. Si $A,B\subset\Bbb{R}$ , entonces $A+B=\{a+b:\ a\in A,\, b\in B\}$ , es decir, la suma de dos conjuntos es el conjunto formado por todas las posibles sumas de un elemento del primero y otro del segundo.

En nuestro caso, vamos a sumar dos veces el Conjunto de Cantor, por lo que la suma será el conjunto de todas las posibles sumas de dos elementos de dicho conjunto. Pero… ¿cómo son estos números? Pues como dijimos al principio, el Conjunto de Cantor está formado por todos los números de $[0,1]$ que se pueden expresar en base 3 mediante un decimal que sólo contiene el 0 y el 2, nunca el 1; dicho de otra forma, un número $x\in[0,1]$ está en $C$ si $\displaystyle x=\sum_{k=1}^\infty \frac{a_n}{3^n}$ donde $a_n\in\{0,2\}$ para cada $n\in\Bbb{N}$ . Así pues, podemos afirmar que $\displaystyle \frac{1}{2}C:=\left\{\sum_{k=1}^\infty \frac{a_n}{3^n}:\ a_n=0,1\right\}$ y, por lo tanto,

$\displaystyle\frac{1}{2}C+\frac{1}{2}C=\left\{\sum_{k=1}^\infty \frac{a_n}{3^n}+\sum_{k=1}^\infty \frac{b_n}{3^n}:\ a_n,b_n=0,1\right\}= \left\{\sum_{k=1}^\infty \frac{c_n}{3^n}:\ c_n=0,1,2\right\}$

pero es que este último conjunto no es más que el propio intervalo $[0,1]$ . Claro, se trata de todos los números que se pueden expresar, en base 3 mediante un decimal en el que aparecen el 0, el 1 ó el 2… o sea, todos.

Así que $\displaystyle \frac{1}{2}C+\frac{1}{2}C=[0,1]$ , por lo que, multiplicando por 2, se deduce la sorprendente propiedad: $C+C=[0,2]$ .

¿Que por qué es sorprendente? pues fíjate que, con la misma regla de suma, se tiene que $[0,1]+[0,1]=[0,2]$ , pero resulta que el Conjunto de Cantor es más pequeño que el intervalo $[0,1]$ . Así tenemos dos conjuntos, uno mucho más pequeño que el otro, pero cuya suma es la misma.

¿Finalizamos con una curiosidad histórica?

Aunque el Conjunto de Cantor debe su nombre y su fama al matemático ~~francés~~ alemán (aber natürlich stammte Cantor aus Deutschland) George Cantor, el descubrimiento (o su primera aparición pública) de este conjunto no es mérito suyo, sino de Henry J. Stephen Smith. este matemático británico, en un artículo titulado On the Integration of Discontinuous Functions (Proc. London Math. Soc. (1874) s1-6 (1): 140-153. doi: 10.1112/plms/s1-6.1.140) introduce el siguiente tipo de conjunto, extremadamente parecido al Cantor actual.

Sea $m$ un número entero mayor que 2. Se divide el intervalo $[0,1]$ en $m$ iguales y se exime al último segmento de cualquier división subsiguiente. Se dividen cada uno de los $m-1$ segmentos restantes en m partes iguales y se eximen los últimos segmentos de cualquier división subsiguiente. Si esta operación se continúa hasta el infinito, se obtiene una cantidad infinita de puntos en el intervalo $[0,1]$ .

Sin embargo, no es hasta 1883 cuando Cantor introduce el conjunto que lleva su nombre. En una serie de seis artículos, que van desde 1879 hasta 1884, que llevan por título Über unendliche, lineare Punktmannichfaltigkeiten y publicados en los Matematische Annalen, Cantor, en el quinto de ellos y en los apéndices o notas al margen del artículo, incluye lo que hoy conocemos como Conjunto de Cantor como un ejemplo concreto de Conjunto Perfecto. De hecho, la definición original es la del conjunto de puntos expresables como $\displaystyle x=\sum_{n=1}^{\infty}\frac{a_n}{3^n}$ donde cada $a_n$ toma los valores 0 ó 2. Aquí os dejo una imagen del la flamante primera aparición:

Definición original del Conjunto de Cantor

Es decir, nada de eliminar segmentos ni cosas así. La definición de Cantor es la de los números que se pueden expresar como decimal en base 3 sin contener el 1.

…y aún hay mucho más

Lo bueno del Conjunto de Cantor es que da para mucho más. Existen muchas cosntrucciones muy similares a estas y que llevan a propiedades aún más curiosas. Por ejemplo, tenemos el Copo de Nieve de Koch, que es una curva cerrada de longitud infinita que encierra un área finita; o la esfera cornuda de Alexander, que es una superficie cerrada en $\Bbb{R}^3$ que divide al espacio en dos partes (la de dentro y la de fuera) que no son topológicamente equivalentes al interior y exterior de la esfera tradicional; o la alfombra de Sierpinski, euivalente 2D al conjunto de Cantor; o la esponja de Menger, que sería la versión 3D.

Pero lo mejor de todo es que todo ello lo tienes al alcance de unos cuantos clicks, en la pantalla de tu ordenador. Ahora es tu momento: adéntrate en el mundo de Cantor y aprende Matemáticas.

Bibliografía

Curiosidades sobre el conjunto de Cantor, M. Macho, en Un paseo por la geometría 1999/2000.
Integración de Funciones de varias variables, J.A Facenda-Aguirre y F.J. Freniche-Ibáñez, Ed. Pirámide, 2002.
La dimensión fractal, M. Zapata Ros, http://platea.pntic.mec.es/mzapata/tutor_ma/fractal/dim_frac.htm.
Fractales en la red, A. Agea y B. Luque, http://www.dmae.upm.es/cursofractales/
Mi puto cerebro matemático, Journal of my Fucking Brain.

PD: Esta entrada participa en la Edición 2.7 del Carnaval de Matemáticas cuyo anfitrión es La Aventura de la Ciencia.

Tito Eliatron

Tito Eliatron (José A. Prado-Bassas) es profesor de matemáticas en la Universidad de Sevila y autor del blog Tito Eliatron Dixit. Desde allí, intenta que cualquier persona sea capaz de entender que, tras muchas situaciones habituales, se esconde un maravilloso mundo matemático que nos explica o nos ayuda sin pedirnos nada a cambio. En resumen, profesor de profesión, divulgador de afición y matemático de devoción.»