Estudié matemáticas, sí, por lo de la belleza suprema, ya saben, a cada uno le da por algo.
Pues bien, todo son risas y geometría computacional hasta que la profesora de tu vástago te pide que vayas a clase a contarle a los niños de 3 años a qué te dedicas.
Claro que existe la opción de decirles que eres profesora, como su ‘seño’ y que enseñas cosas de los números y de los triángulos, cuadrados y círculos. Pero no es eso lo que hago, ¡eso es mucho más difícil!.
Así que, entendiendo que los niños tienen muy clara la proporción directa entre proximidad y pertenencia, me lié la manta a la cabeza y decidí hablarles sobre Diagramas de Voronoi (contando con la experta e inestimable colaboración del padre de la criatura, mi santo, matemático también).
¿Qué es un diagrama de Voronoi?
Pues… es una descomposición de un espacio métrico en regiones, asociada a la presencia de objetos, de tal forma, que en dicha descomposición, a cada objeto se le asigna una región del espacio métrico formada por los puntos que son más cercanos a él que a ninguno de los otros objetos.
Lo que se dice dividir el espacio en tantas regiones como puntos u objetos tengamos de tal forma qu ea cada punto le asignemos la región formada por todo lo que está más cerca de él que de nadie.
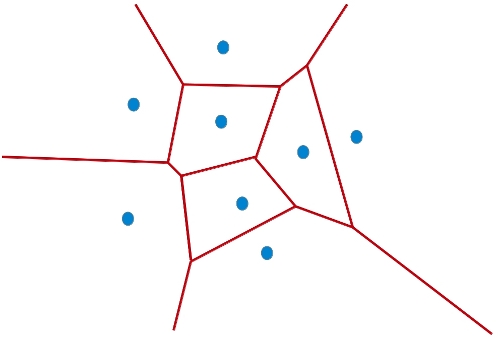
Por ejemplo, si tenemos un conjunto de 8 puntos en el plano euclídeo, su diagrama de Voronoi es una partición del plano de este estilo:
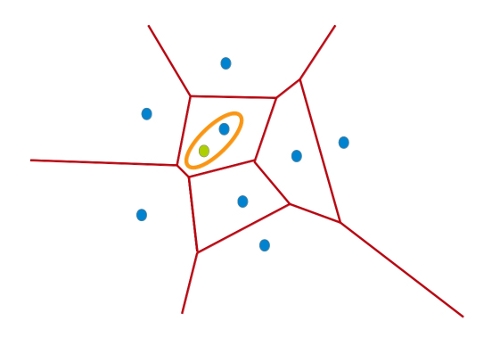
Ante la presencia de un nuevo punto, por ejemplo, el verde en la siguiente figura, es inmediato reconocer cuál de los 8 originales es el más cercano a él. El punto generador de la región en la que ha caído.
 Esta propiedad del Diagrama de Voronoi tiene aplicaciones inmediatas, tales como encontrar el ‘restaurante’ de comida rápida de alguna famosa cadena más cercano a tu ubicación, por ejemplo, si andas de paseo por París
Esta propiedad del Diagrama de Voronoi tiene aplicaciones inmediatas, tales como encontrar el ‘restaurante’ de comida rápida de alguna famosa cadena más cercano a tu ubicación, por ejemplo, si andas de paseo por París
Pero, claro, ésta no es la forma, posiblemente, de plantearlo en la clase de tres años. Para ellos lo planteamos como una cuestión de propiedad de caramelos.
«Imaginaos» les dije «que los Lunnis están en el patio del recreo, cada uno en un sitio. Y que de pronto, alguien descubre un caramelo, como en esta figura»
«¿De quién es ese caramelo?»
Como era de esperar todas las respuestas fueron inducidas por la ley de ‘del que esté más cerca’. Pero había dudas entre Lucho (el amarillo), Lublú (el azul) y Lubina (la bruja), que eran los tres más próximos.
Era mi momento.
El diagrama de Voronoi sirve para dividir el patio en regiones, de forma que cada Lunni sabrá que todo lo que esté en su región está más cerca de él que de ninguno de sus amiguitos.
«Vamos a construir el diagrama de Voronoi del patio de los Lunnis, a ver quién se queda el caramelo»
«¡De Lucho!» gritaron todos, algunos arriesgando las paredes de las venitas de sus cuellos. Luego seguimos ‘lanzando’ caramelos en distintas regiones y ellos gritando el nombre del agraciado.
No sé si alguno recuerda algo de aquel día, pero parecían pasárselo bien.
Ahora bien, aparte de resolver conflictos en el patio de un colegio o de orientarte en la búsqueda de una hamburguesa, ¿qué son y para qué se utilizan los diagramas de Voronoi?
En primer lugar, dejadme que os cuente que esta estructura que recibe el nombre de Georgy Voronoi, matemático ruso, también es conocida con los nombres de Polígonos de Thiessen (en honor de Alfred Thiessen, meteorólogo estadounidense) o Teselación de Dirichlet (por el matemático Gustav Lejeune Dirichlet). Y seguro que muchos más, puesto que es una estructura tan lógica e intuitiva que aparece cada vez que uno se plantea cuestiones relacionadas con problemas de proximidad.
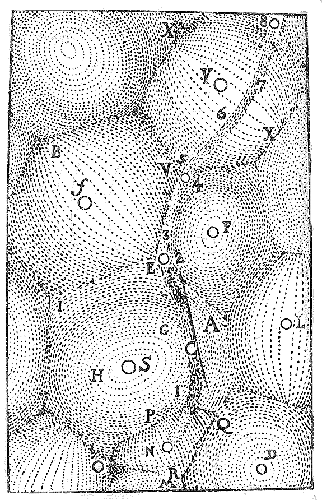
Pero aunque mi contacto con los diagramas de Voronoi está ligado al estudio de Geometría Computacional, disciplina relativamente joven, hay autores que señalan el uso de la citada estructura en trabajos de Descartes de 1644 sobre el cielo, cuando afirmaba que el Universo estaba plagado de éter y materia y formado por vórtices.
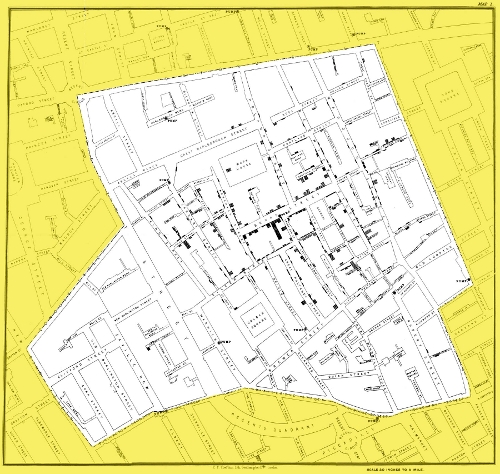
 Eso sí, sin duda, desde el punto de vista histórico, una aplicación del diagrama de Voronoi digna de mención, aparece en el análisis de John Snow, para muchos el padre de la epidemiología moderna, del brote cólera que azotó Londres en 1854.
Eso sí, sin duda, desde el punto de vista histórico, una aplicación del diagrama de Voronoi digna de mención, aparece en el análisis de John Snow, para muchos el padre de la epidemiología moderna, del brote cólera que azotó Londres en 1854.
Por aquel entonces no se conocía con exactitud la etiología ni el método de trasmisión de la citada enfermedad, y se debatían entre dos posibilidades: el contagio por contacto con el enfermo, sus ropas y/o pertenencias; y la teoría miasmática que atribuían la trasmisión a condiciones atmosféricas, como los vientos. Snow usó el método geográfico deduciendo que la causa de la enfermedad era el consumo de aguas contaminadas por heces. Para ello, en un mapa, señaló la distribución de muertes por cólera.
A continuación, estudió la distribución de las fuentes de agua potable de la ciudad y delimitó las regiones de Voronoi de cada una de esas bombas. Calculando la distancia entre la residencia de cada difunto y la bomba de agua más cercana, llegó a la conclusión de que la zona afectada más por el cólera correspondía con la región de Voronoi asociada a la bomba de Broad Street, ya que en su región se dieron 73 de 83 casos.
Tras retirar la manija de la citada bomba, el brote de cólera se extinguió. Ea, para que digan que las matemáticas no sirven para nada… Eso sí, Snow no le llamaba regiones de Voronoi por varias razones, entre otras, porque Voronoi no había nacido.
Desde entonces y hasta nuestros días, el diagrama de Voronoi en 2 y 3 dimensiones ha sido utilizado en campos muy diversos. Vamos a ver algunos de ellos.
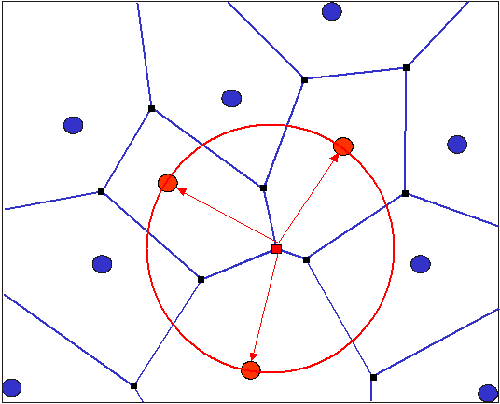
Fijaos que por ejemplo, en Robótica, si tenemos una escena con obstáculos en las que un robot deba moverse, una forma de evitar las colisiones sería diseñar la trayectoria del robot sobre las líneas del diagrama de Voronoi de los obstáculos, con lo que se movería siempre a medio camino entre dos de ellos.
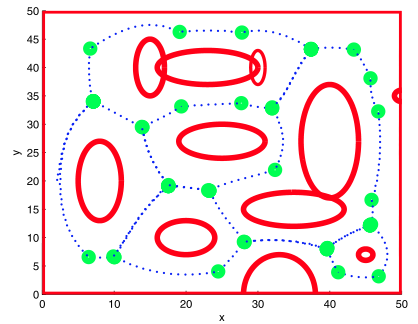
En la figura anterior, los obstáculos, en rojo, y las líneas punteadas azules, los límites de las distintas regiones de Voronoi de los mismos (sí, también se puede calcular el diagrama de Voronoi de otros objetos que no sean puntos). Si el robot camina por las líneas azules, no habrá colisión.
Esta misma estrategia podría ser utilizada en diplomacia para ‘pasear’ entre intereses enfrentados sin dar lugar a suspicacias, pero no me consta que esté muy afinado el algoritmo…
Una idea similar a la del robot, se propone en un trabajo de C.M. Gold de 2006, planteando el uso de esta misma estructura en el ámbito de sistemas de información geográfica, utilizando, de nuevo, las aristas del diagrama para evitar la colisión con los accidentes geográficos.

Otra aplicación de este diagrama, por ejemplo, es el cálculo del mayor círculo vacío.
Imaginemos que los puntos representan núcleos urbanos y que queremos ubicar un servicio indeseable, algo que nadie quiere tener cerca, no sé, por ejemplo, una central nuclear, una fosa de purines o una hamburguesería de alguna cadena popular. Hombre, siempre está la alternativa de mandarla al país vecino, pero eso no está bonito. Vamos a restringir el problema, el servicio indeseado, hay que ubicarlo dentro de la envolvente convexa de los núcleos de población. De manera intuitiva, la envolvente convexa de un conjunto de puntos en el plano, es la forma que adoptaría una goma elástica si la soltáramos alrededor de los puntos, en los que hemos calvado puntillas, en la siguiente figura la tenemos en verde:
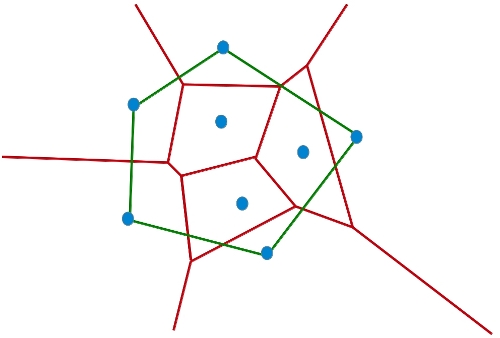
(Sobre el cálculo de la envolvente convexa y la filosofía de la Geometría Computacional escribí hace un tiempo esto para Gaussianos)
En ese caso, para ubicar un servicio chungo dentro de la frontera verde, lo que tenemos que conseguir es que la población más cercana a dicho servicio esté lo más alejada posible de el mismo, es decir, maximizar la mínima distancia a él. Esto se consigue ubicándolo en el centro del mayor círculo vacío de poblaciones que podamos dibujar dentro de la frontera verde. Pues bien, ¡tachán!, ese círculo estará centrado en un vértice del diagrama de Voronoi.
Interesante, ¿no? Pues no se vayan todavía, aún hay más.
Vámonos al bosque. Porque también se ha usado el diagrama de Voronoi como herramienta de investigación forestal para analizar y predecir la influencia del espacio ocupado por los árboles en la evolución de un bosque. Mi colega y amigo Manuel Abellanas de la Universidad Politécnica de Madrid, junto a otros investigadores, ha desarrollado VOREST, la herramienta mencionada.
Eso a nivel macroscópico, pero también a nivel microscópico podemos encontrar trabajos que aplican el diagrama de Voronoi a sus investigaciones. Ya desde 1974, F.M. Richards, biólogo estructural en Yale e innovador en el estudio de las relaciones entre las estructuras de proteínas y sus funciones biológicas, señaló la eficiencia y relevancia de nuestra estructura en 3 dimensiones para la descripción de la estructura de las proteínas.
Entre los numerosos trabajos que podemos encontrar en esa línea, tenemos, por ejemplo, esta herramienta, VORO3D, que permite la visualización en tres dimensiones de la estructura de las proteínas. Para ello, y hablando sin mucho rigor, considera el empaquetamiento de aminoácidos, de forma que cada residuo es representado como un punto del espacio. Como los aminoácidos cercanos a la superficie de la proteína podrían dar lugar a regiones de Voronoi abiertas, se considera la molécula dentro de un recubrimiento de esferas cuyo volumen no difiera demasiado del volumen medio real.

También en Química Computacional, el método de Voronoi Deformation Density (VDD) se usa para calcular la distribución de carga atómica en una molécula, para obtener información sibre sus propiedades químicas.
¿Qué más?
Los huesos. Sí, señor. A grandes rasgos, en nuestros huesos podemos distinguir dos zonas diferenciadas: el hueso compacto y el hueso esponjoso o trabecular.

Existen una importante cantidad de trabajos enfocados a generar modelos en 2 dimensiones que representen la arquitectura trabecular de los huesos, usando diagramas de Voronoi, tomando como puntos en este caso, los centros de los poros del hueso esponjoso.

Pero aparte de la utilidad de este tipo de estructuras, no me negaréis la belleza y armonía geométrica de las mismas. Belleza que no parece haber pasado desapercibida par arquitectos y diseñadores:

¿Una ciudad dentro del rascacielos Voronoi?

Pero un concepto tan natural e intuitivo como éste, el de vecindarios alrededor de algún punto destacada por alguna razón, debe ser encontrado también en la naturaleza, ¿no?
Cuando encuentro formas similares en el ámbito natural me gusta jugar a pensar qué puntos son los generadores de esos posibles diagramas de Voronoi, qué tienen de especial para aglutinar a otros en sus proximidades.
¿Algunos pelos más gordotes que el resto?
¿Los últimos puntos con algo de humedad?
¿Los puntos más calientes de la superficie del Sol?
¿O el último trozo de hielo?
Tengo que parar en algún momento, pero hay infinidad de aplicaciones prácticas y motivos naturales relacionados con los diagramas de Voronoi. Están ahí fuera, esperando que los descubráis, ¿a qué esperáis?
Ya me iréis contando, estaré por aquí. O por allí.
PD: Esta entrada participa en la Edición 2.9 del Carnaval de Matemáticas, cuyo anfitrión es el blog Que no te aburran las M@TES.
Soy profesora del área de Matemática Aplicada de la Universidad de Sevilla desde un maravilloso día soleado de Noviembre de 1995. Desde entonces he descubierto que la satisfacción de investigar es sólo comparable a la de contar y enseñar lo que has descubierto. Durante más de 10 años esto último se redujo al ámbito de mis clases en la Universidad y a las comunicaciones en congresos. Con la llegada de mis enanos se me planteó el reto de contarlo fuera del aula, en la alfombra del salón. Y oye, me gustó. Ahora dedico parte de mi tiempo libre a la divulgación, para niños de 9 a 99 años, consciente de que a todo el mundo le gustan las matemáticas, solo que algunos aún no lo saben. Mis coordenadas en: claragrima.com.