
Hace algún tiempo os contaba en este mismo blog mi primera actuación como mamá matemática en la clase del mayor de mis hijos, cuando éste tenía 3 años. Pues bien, tras el éxito obtenido con el diagrama de Voronoi y su indiscutible utilidad para el reparto justo de caramelos, me crecí y desde entonces he seguido visitando,cada vez que puedo y me invitan, las clases de mis dos hijos, para hacer shows matemáticos.
En esta gira artística, hace unos meses, otra vez en la clase del mayor, 5º de primaria, (cómo pasa el tiempo…), presenté el Teorema de los cuatro colores, esta vez con la ayuda de Mati, nuestro pequeño proyecto de divulgación para niños.
Para esta ocasión el planteamiento fue el siguiente:
“Si dibujáis un mapa con provincias, por muy, muy difícil y enrevesado que lo dibujéis, yo lo puedo colorear bien usando sólo 4 colores diferentes.
Entendiendo por colorear bien que si dos provincias comparten un trozo de frontera por muy, muy poco que compartan, ésas deben ser coloreadas con colores distintos.”
Como siempre, la curiosidad de los niños no tardó en aparecer y uno ellos preguntó: “Y si sólo tiene 3 provincias, ¿cómo vas a usar los 4 colores?”
Ésa era fácil.
El teorema de los 4 colores asegura que cualquier mapa, como máximo, necesita 4 colores para ser bien dibujado, pero no siempre son necesarios. “Pensad por ejemplo en un país formado sólo por islas. En ese caso, con un sólo color sería suficiente.”
La siguiente pregunta no tardó en ser planteada: “ Y España, ¿necesita los 4 colores?”
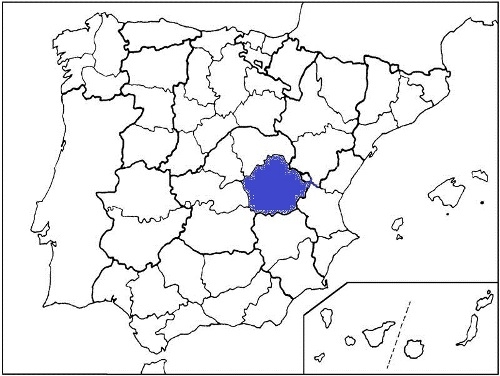
Para ésta también estaba preparada, de hecho en el capítulo de Mati que iba a presentar en unos minutos, se explicaba por qué España necesita usar los 4 colores, ni uno menos, para ser bien coloreada. Para ello, nos fijábamos en Cuenca y la coloreábamos de azul.
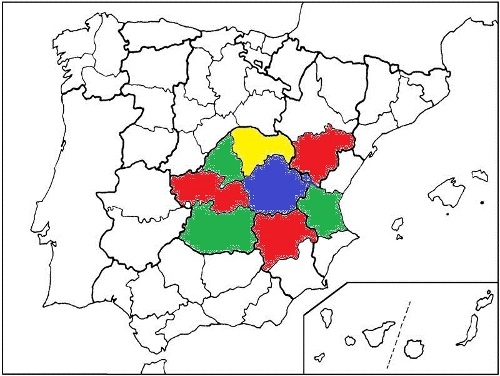
 Al tratar de colorear las provincias que rodean a Cuenca, empezamos usando dos colores, de forma alternada, rojo y verde. Pero como el número de provincias que rodean a Cuenca es impar, para cerrar ese ciclo, necesitamos un nuevo color, que no puede ser ni rojo, ni verde, ni tampoco azul. Lo que nos obliga a emplear el cuarto color para Guadalajara. El amarillo, por ejemplo.
Al tratar de colorear las provincias que rodean a Cuenca, empezamos usando dos colores, de forma alternada, rojo y verde. Pero como el número de provincias que rodean a Cuenca es impar, para cerrar ese ciclo, necesitamos un nuevo color, que no puede ser ni rojo, ni verde, ni tampoco azul. Lo que nos obliga a emplear el cuarto color para Guadalajara. El amarillo, por ejemplo.
 Éste es uno de las primeros hechos que se explican cuando se habla en Teoría de Grafos, de coloreado de éstos: Todo ciclo de longitud impar, necesita 3 colores para ser colorado. Donde, cuando decimos un ciclo, nos referimos a una secuencia de aristas y vértices conectados en forma circular.
Éste es uno de las primeros hechos que se explican cuando se habla en Teoría de Grafos, de coloreado de éstos: Todo ciclo de longitud impar, necesita 3 colores para ser colorado. Donde, cuando decimos un ciclo, nos referimos a una secuencia de aristas y vértices conectados en forma circular.
 Mientras que si el ciclo tiene un número par de vértices, sólo 2 colores serán necesarios y suficientes, como podemos ver en la figura siguiente.
Mientras que si el ciclo tiene un número par de vértices, sólo 2 colores serán necesarios y suficientes, como podemos ver en la figura siguiente.
 Huy, es cierto… He pasado de hablar de coloreado de mapas a coloreado de grafos sin justificarlo. Voy a tratar de hacerlo con una imagen por aquello de que éstas valen más que no sé cuántas, pero muchas palabras. Si en el mapa de la comunidad andaluza, por ejemplo, ponemos un vértice por cada provincia y una arista entre dos provincias si éstas son limítrofes, nos quedará el siguiente grafo.
Huy, es cierto… He pasado de hablar de coloreado de mapas a coloreado de grafos sin justificarlo. Voy a tratar de hacerlo con una imagen por aquello de que éstas valen más que no sé cuántas, pero muchas palabras. Si en el mapa de la comunidad andaluza, por ejemplo, ponemos un vértice por cada provincia y una arista entre dos provincias si éstas son limítrofes, nos quedará el siguiente grafo.
 Colorear ese grafo consiste en asignar colores a los vértices (puntos) de forma que no haya vértices unidos con el mismo color. Andalucía nos sale con sólo 3 colores y no con menos de 3, porque para Sevilla, Huelva y Cádiz ya necesitamos 3.
Colorear ese grafo consiste en asignar colores a los vértices (puntos) de forma que no haya vértices unidos con el mismo color. Andalucía nos sale con sólo 3 colores y no con menos de 3, porque para Sevilla, Huelva y Cádiz ya necesitamos 3.
 Ea, pues ya lo tenemos. Asignamos el color de los vértices del grafo a la correspondiente provincia y hemos terminado.
Ea, pues ya lo tenemos. Asignamos el color de los vértices del grafo a la correspondiente provincia y hemos terminado.
 Volvamos a la clase de 5º de primaria.
Volvamos a la clase de 5º de primaria.
La mejor pregunta de todas fue “¿Por qué quieres usar pocos colores? ¿No quedaría más mono con más colorido?”
Esta pregunta era la más interesante de todas y confieso que, muchas veces, la he echado de menos cuando explico Matemática Discreta a mis estudiantes en la Universidad. Es entonces cuando me reafirmo en mi teoría de que los niños son curiosos por naturaleza y a medida que crecen esa curiosidad se va desvaneciendo, o cambia de interés, porque a partir de cierta edad la pregunta casi siempre es “¿Esto cae en el examen?”
El reto de responder esa pregunta no era fácil con unos alumnos de primaria, pero no podía dejar aquella pregunta sin responder.
Vamos a ello.
Y así, de paso, os explico por qué y para qué la Teoría de Grafos se ha dedicado y se dedica a colorear grafos con el mínimo número de colores posibles.
Una vez convencidos de que colorear mapas es colorear grafos, la siguiente prueba era mostrarles que no se trataba de una cuestión sólo estética sino de optimización de recursos.
“Imaginaos que vamos a trasladar a los animales del zoo de Central Park (famosos en el ‘mundo mundial’ tras la película Madagascar, una de mis favoritas) al mundo salvaje. Excepto Alex, el león que es un ególatra que aún no ha descubierto que los filetes que se come son de carne animal, no es posible transportar en la misma jaula a animales carnívoros con sus víctimas, ¿verdad?”
 Inventé sobre la marcha, no me preguntéis cuáles, algunas relaciones de compatibilidad e incompatibilidad entre los habitantes del zoo hasta que construimos la siguiente tabla:
Inventé sobre la marcha, no me preguntéis cuáles, algunas relaciones de compatibilidad e incompatibilidad entre los habitantes del zoo hasta que construimos la siguiente tabla:
 En la tabla anterior, debajo de cada nombre, hemos listado los nombres de los animales que no podrán viajar con él en la misma jaula.
En la tabla anterior, debajo de cada nombre, hemos listado los nombres de los animales que no podrán viajar con él en la misma jaula.
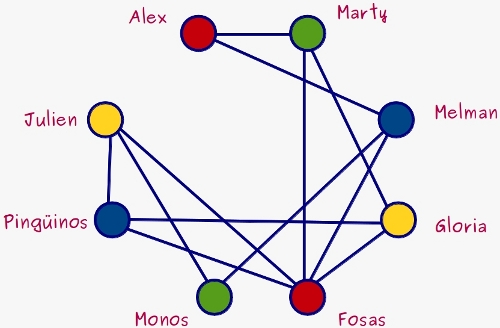
Queremos hacer ese transporte de animales usando el mínimo número posible de jaulas, porque cada jaula es muy cara y estamos en crisis. Para ello vamos a dibujar un grafo: cada animal lo dibujamos como un puntito, un vértice del grafo, y dibujaremos una arista entre dos vértices si éstos representan a dos animales que NO pueden compartir jaula.
Ya está. Si conseguimos colorear bien ese grafo, ya tenemos una posible solución para el problema de las jaulas. ¿Por qué? Porque si por ejemplo, a una animal (vértice) se le asigna el color rojo, ninguno de los animales incompatibles con él tendrá el color rojo, porque estarían unidos a él por aristas. Si usamos 7 colores, significará que necesitamos sólo 7 jaulas para hacer bien el transporte sin que nadie se coma a nadie. En el grafo de nuestra tabla nos salió, entre todos, con 4colores.
 Una felicidad inundó el aula y aquellos ojillos me miraban… brillantes. No hay mejor motor para seguir enseñando. Había que aprovechar aquel terreno abonado para seguir sembrando…
Una felicidad inundó el aula y aquellos ojillos me miraban… brillantes. No hay mejor motor para seguir enseñando. Había que aprovechar aquel terreno abonado para seguir sembrando…
“¿Pero seguro que no podemos colorear con menos colores?”
Porque si podemos, nos ahorramos jaulas y transportar jaulas es algo carísimo… Otra vez, entre todos, volvimos a colorear el grafo y … sí, aún podíamos usar una jaula menos.
 No sé si se acordarán mucho tiempo de para qué sirve el coloreado de grafos, pero quiero pensar, por lo que veía en sus carillas que se lo estaban pasando muy bien.
No sé si se acordarán mucho tiempo de para qué sirve el coloreado de grafos, pero quiero pensar, por lo que veía en sus carillas que se lo estaban pasando muy bien.
Pues de eso se trata, de ahorrar en jaulas en el caso de Madagascar y de otros recursos en otros problemas, o de organizar horarios, distribuir asignaturas y profesores… Y por eso, y por otros problemas similares, en Teoría de Grafos se ha estudiado y se estudia el número cromático de un grafo, es decir, el número mínimo de colores necesarios para colorar sus vértices.
Lo sorprendente en una primera lectura de este tipo de problemas tan sencillos de plantear y de entender su solución cuando te la muestran, es que es un problema, desde el punto de vista algorítmico, NP completo. Y esos son problemas, muy, muy difíciles, creedme. Pero a mí, ¡me encantan!
Sí. No es tan sencillo eso de coger la caja de lápices de colores y colorear grafos, al menos, no tanto como parece.
Ya metida en faena, y con lo que me gusta, les conté que un problema parecido pero distinto, sería colorear las aristas del grafo, de forma que de un vértice no puedan salir dos aristas del mismo color.
“Y eso, ¿para qué sirve?”
Pues fijaos, imaginaos que tenemos que hacer un torneo de ajedrez aquí en vuestra clase, a la hora del recreo. Sois 24, ¿no? Cada alumno tiene que enfrentarse a todos sus compañeros, pero en cada recreo, sólo puede enfrentarse a uno de ellos.
“¿Y si no acabamos en el recreo?”
Venís por la tarde ese día. La pregunta es ¿cuántos recreos durará el campeonato?
Ahora los vértices del grafo son los alumnos de la clase y cada arista representa una partida de ajedrez. Tendremos 24 vértices y de cada uno saldrán 23 aristas, una por cada compañero. Si le damos color a las aristas de forma que de ningún vértice salgan dos aristas del mismo color, cada uno de los colores asignados representará un recreo, porque estará emparejando a alumnos distintos.
Es fácil ver que vamos a necesitar, por lo menos, 23 colores, porque de cada vértice salen 23 aristas y deben ser pintadas con colores distintos. Pero, ¿serán suficientes 23? ¿O necesitamos más?
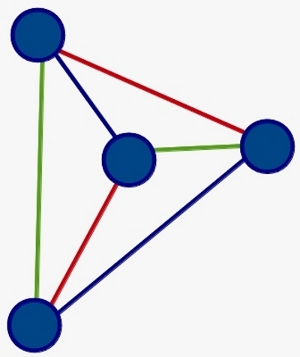
Hicimos el ejemplo con 4 niños nada más, porque pintarlo con 24, aparte de tedioso, era visualmente menos claro. Y sí, con 4 niños, bastaban con 3 recreos, es decir, se podían colorear la aristas del grafo con sólo 3 colores.
 ¿Y si son 5? ¿Bastan 4 colores? Vamos a intentarlo. Usamos el rojo para emparejar a 4 niños, el 5º niño descansa ese recreo. Luego el azul para emparejar a otros 4 y dejando descansar a un 5º. Luego el verde, el amarillo…
¿Y si son 5? ¿Bastan 4 colores? Vamos a intentarlo. Usamos el rojo para emparejar a 4 niños, el 5º niño descansa ese recreo. Luego el azul para emparejar a otros 4 y dejando descansar a un 5º. Luego el verde, el amarillo…
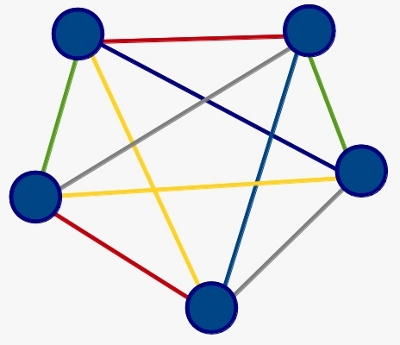 Pues no, parece que no bastan 4 colores, nos faltan 2 aristas (en gris) sin colorear y ya no podemos usar ninguno de los 4 que hemos usado. Necesitamos un 5º color.
Pues no, parece que no bastan 4 colores, nos faltan 2 aristas (en gris) sin colorear y ya no podemos usar ninguno de los 4 que hemos usado. Necesitamos un 5º color.
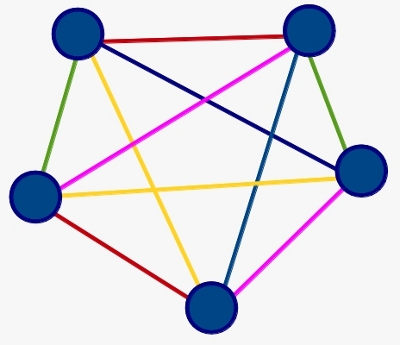 ¿Qué ha pasado? Pues que si el número de participantes en el torneo, liga o campeonato es par, el número de jornadas que se necesitan es uno menos. Para 24 niños, con 23 jornadas es suficiente. Pero si el número de participantes es impar, necesitamos tantas jornadas como participantes y en cada una de ellas, uno de estos participantes estará descansando. Es decir, para 25 niños, necesitamos 25 jornadas.
¿Qué ha pasado? Pues que si el número de participantes en el torneo, liga o campeonato es par, el número de jornadas que se necesitan es uno menos. Para 24 niños, con 23 jornadas es suficiente. Pero si el número de participantes es impar, necesitamos tantas jornadas como participantes y en cada una de ellas, uno de estos participantes estará descansando. Es decir, para 25 niños, necesitamos 25 jornadas.
Sí, el coloreado de aristas también tiene su gracia, ¡hasta para organizar Eurovisión! Y sí, también conduce a problemas NP completos...
Quiero pensar que cuando terminé les había convencido de la importancia de ahorrar colores en el coloreado de grafos, tanto de vértices, para ahorrar en jaulas, como de aristas, para que los campeonatos no sean eternos.
Eso sí, esta obsesión por trabajar con pocos colores sólo me agrada si hablamos de grafos. En la vida me gusta que la gente que me rodea, la que me encuentro por las calles de mi ciudad, de mi país o cuando estoy de turismo, tengan todos los colores posibles. Porque lo que hace que esto de vivir sea tan enriquecedor y emocionante es que cada uno tenga su color especial.
Este artículo participa en la 3,1415 edición del Carnaval de Matemáticas que organiza Gaussianos.
Soy profesora del área de Matemática Aplicada de la Universidad de Sevilla desde un maravilloso día soleado de Noviembre de 1995. Desde entonces he descubierto que la satisfacción de investigar es sólo comparable a la de contar y enseñar lo que has descubierto. Durante más de 10 años esto último se redujo al ámbito de mis clases en la Universidad y a las comunicaciones en congresos. Con la llegada de mis enanos se me planteó el reto de contarlo fuera del aula, en la alfombra del salón. Y oye, me gustó. Ahora dedico parte de mi tiempo libre a la divulgación, para niños de 9 a 99 años, consciente de que a todo el mundo le gustan las matemáticas, solo que algunos aún no lo saben. Mis coordenadas en: claragrima.com.


