En la tradición científica occidental, ha habido un largo debate sobre la aplicabilidad de las matemáticas a la naturaleza. La cuestión es si el mundo es fundamentalmente matemático, en cuyo caso el análisis matemático es el camino más seguro para una comprensión más profunda, o si las matemáticas son aplicables sólo a los aspectos superficiales cuantificables de las cosas, sin alcanzar realidades últimas). Desde el Renacimiento hasta nuestros días, este debate parece haberse decantado hacia la primera opción.
Ya en la Antigüedad, podemos tomar a Pitágoras y Platón como los que tomaban el mundo de manera eminentemente matemática, y por otro lado a Aristóteles, el que tenía en cuenta las cualidades físicas de la realidad además de las matemáticas.
En el siglo 4 a.C, las conquistas de Alejandro Magno pusieron en contacto a los griegos con las matemáticas de los pueblos orientales, y esto desembocó en la fundación de la Biblioteca de Alejandría, donde los sabios de la época se ocupaban del estudio de unas ciencias mixtas, mezcla de física y matemáticas. Entre estas ciencias, se encontraba la estática. Esta rama de la mecánica se puede plantear como la búsqueda del equilibrio de los cuerpos en un sistema. Desde el principio, uno de los problemas principales que se estudió fue el de la balanza romana, cuya generalización es el problema de la palanca. Este sistema se vio que era común en la mayoría de máquinas y mecanismos principales de la época.
Hoy en día, cualquier estudiante de física de secundaria debería saber que el equilibrio en ese sistema se consigue por igualdad de momentos a ambos lados del centro de giro de la palanca. Es decir,
Peso1·distancia1 = Peso2·distancia2.
Momento se define habitualmente como fuerza por distancia, y normalmente se calcula el momento en un eje, o en su caso, en un punto sobre un plano.
Sin embargo, no existía todavía el concepto de momento en aquella época y tardó bastantes siglos más en llegar, por la que los primeros eruditos se las tuvieron que apañar para resolver este problema. Como ya se ha dicho, había división en el planteamiento de problemas, y los matemáticos tendían a estudiar la mecánica eliminando las consideraciones dinámicas (las fuerzas o causas) para concentrarse en el equilibrio (sin fuerzas netas), mientras que los físicos tendían a tomar en cuenta los movimientos y sus motores, con lo que sus esfuerzos eran difíciles de geometrizar, ya que el estudio matemático del movimiento estaba por hacer.
La pregunta que se hizo Arquímedes (siglo III a.C) era “¿por qué pequeñas fuerzas pueden levantar grandes pesos en una palanca?” y desarrolló su física a través de los pesos: los círculos de Arquímedes.
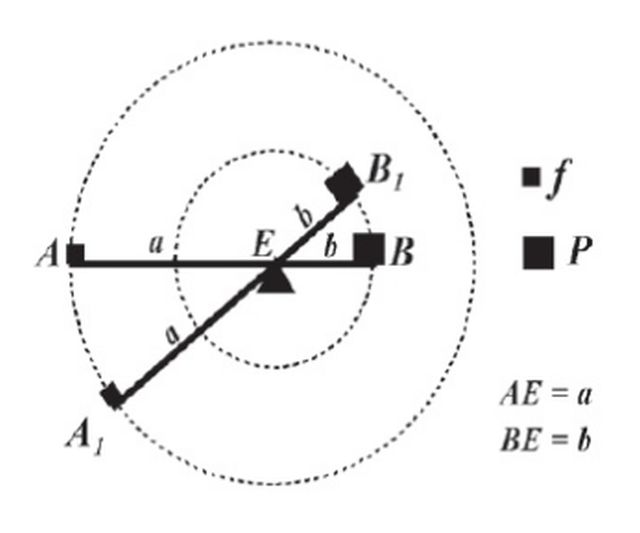 Arquímedes enunció su ley así: la razón entre el peso movido P al peso que causa el movimiento f es igual a la razón inversa de las distancias desde el centro.
Arquímedes enunció su ley así: la razón entre el peso movido P al peso que causa el movimiento f es igual a la razón inversa de las distancias desde el centro.
Representa la idea inicial para el concepto de momento. La teoría física y matemática para la resolución de la palanca lo plasmó en el libro Sobre el equilibrio de los planos.
Concretamente, en el segundo corolario recogido en esta obra hay una idea fundamental que siglos después fue puesta en duda. El corolario afirmaba así:
Si hay un número par de magnitudes con sus centros de gravedad situados a iguales distancias sobre una línea recta y si las dos del medio son iguales, mientras que aquellas que equidistan entre sí (a cada lado) son iguales respectivamente, el centro de gravedad del sistema es el punto medio de la línea que une los centros de gravedad de los dos del medio.
Y la idea clave a la que dio lugar fue la siguiente:
- Consideremos una barra sin peso dividida en 6 tramos equidistantes que se aguanta sobre su punto medio. Además, pensemos en dos pesos: uno compuesto por cuatro unidades y otro compuesto por 2 unidades de peso (cada bloque rojo y azul pesa lo mismo).
- Colocamos las 6 unidades en el punto medio de cada tramo. El sistema está en equilibrio.
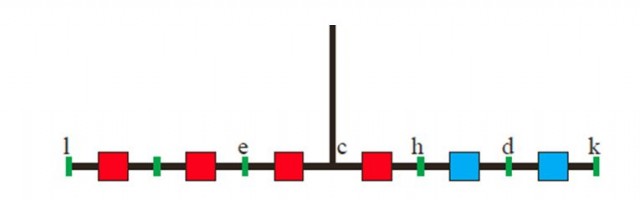 Ahora consideremos que sigue habiendo equilibrio si hacemos lo siguiente:
Ahora consideremos que sigue habiendo equilibrio si hacemos lo siguiente:
 De manera que tendríamos algo así:
De manera que tendríamos algo así:
Esto ocurrió en el siglo III a.C. y nos tenemos que ir hasta el XIX para conocer al que se considera uno de los grandes filósofos de la ciencia: Ernst Mach. Probablemente, este hombre sea más conocido por el número que lleva su nombre o sus estudios de ondas de choque, entre otras ideas. Pero Mach fue sobre todo un crítico de la mecánica de Newton. Su obra más importante es Science of Mechanics, que representa un ensayo de sus ideas y razones para dudar. Mach, como filósofo, tuvo influencia del positivismo, lo cual significa que solo creía en conceptos que se pudieran percibir por lo sentidos como única fuente del conocimiento y único medio para descubrir la verdad en la ciencia. Es conocida la crítica que hizo a la demostración de Arquímedes sobre la palanca Concretamente el extracto es:
De la mera suposición del equilibrio de iguales pesos a iguales distancias, se deduce la proporcionalidad inversa entre los pesos y los brazos de palanca! ¿Cómo es esto posible?
Si el mero hecho de que el equilibrio depende del peso y de la distancia, lejos de poder deducirlo lógicamente, tuvimos que buscarlo en la experiencia, muchos menos podrá encontrarse, con recursos puramente especulativos, la forma de esa dependencia, vale decir la proporcionalidad inversa.
En verdad, Arquímedes y todos sus sucesores, tácitamente o en forma más o menos oculta, introdujeron la hipótesis de que el efecto perturbador del equilibriode un peso P a una distancia D está medido por el producto P×D – el llamado momento estático.

Lo que nos quiere decir Mach es que si la dependencia del momento con D no fuera lineal, no serían válidas las transformaciones que hemos visto en los gráficos de la sección anterior. Es decir, la dependencia lineal P×D ya está supuesta desde el inicio en la demostración. Para entender la afirmación del austríaco, hay que tratar de imaginarse los escasos fundamentos mecánicos con los que contó Arquímedes para establecer su ley. Sin embargo, Mach fue rebatido por otros historiadores de la ciencia (como Valiati y Hölder) y hoy en día se publican aún artículos científicos argumentando las distintas ideas de los eruditos (Palmieri, 2007) o éste, de 2008.
Sin embargo, no deja de ser sorprendente que entre tantos siglos de diferencia, haya habido científicos que se han ocupado del problema de la palanca, como Galileo, Stevinus o Da Vinci. Cada uno de ellos introdujo distintos conceptos para la resolución del problema según la manera en la que veía la física, y también incorporaron la visión dinámica y cinemática, la cual no podemos atribuírsela a Arquímedes. Sin embargo, lo que sí que podemos atribuirle es el comienzo del estudio de la Mecánica, historia que tiene más de dos milenios de duración. En el debate entre quién tenía razón entre Mach y Arquímedes, hay una tendencia favorable al griego, sobre todo basándose en otro estudio clásico de la Antigüedad, realizado por Euclides.
En la historia de la Mecánica se distinguen 6 periodos:
1- Es la época en la que la Mecánica consistía solo en observaciones, sin ningún tipo de documentación ni plasmar su pensamiento. A pesar de que se puede trazar el origen de ciencias como la astronomía gracias a textos babilonios y egiptos, no existen esas referencias para Mecánica.
2- Problema de la palanca y la aparición de los primeros tratados. Los que más peso tuvieron en esta época fueron Arquímedes, Aristóteles, Herón y Euclides.
3- Es la visión de la mecánica como un conjunto de equilibrios y pesos, en el que la palanca siguió teniendo un papel influyente.
4- El cuarto período es la antesala de la Mecánica Clásica, en el que aparecen los trabajos de Galileo y Leonardo Da Vinci. Se centran en problemas del plano inclinado, muelle, palanca y péndulo sobre todo.
5- Abarca la visión mecánica del mundo y movimiento de los planetas, sobre todo a partir de trabajos de Descartes y Newton.
6- Esta época se caracteriza por la aparición de nuevos conceptos de la física moderna, como la relatividad y la Mecánica cuántica.
De hecho, Einstein dijo de Mach que era el precursor de su teoría de la relatividad. Sin embargo, Mach nunca aceptó estas ideas y se desvinculó de la física moderna, ya que muchas ideas eran muy abstractas para ser válidas según su pensamiento.
Fuentes
Agradecer la participación de @carlcasan en el artículo
La tensión entre la estática y dinámica http://es.scribd.com/doc/59633589/6/La-critica-de-Mach-a-la-demostracion-de-Arquimedes
Renn, J., Damerow, P., and McLaughlin, P. Aristotle, Archimedes, Euclid, and the Origin of Mechanics: The Perspective of Historical Epistemology. Berlin: Max Planck Institute for the History of Science, 2010, pg 1-2
Science of Mechanics. Ernst Mach
Dr. en Ingeniería Informática y profesor en la UPV-EHU. Actualmente, investiga sobre robótica, UAVs e inteligencia artificial.


