Hasta donde yo sé, con mi escasa cultura musical, no se ha escrito ninguna canción dedicada al triángulo. Ni siquiera aparece mencionado en la oda que Javier Krahe (no podía haber sido otro) le dedicó a algunos objetos geométricos:
[youtube]https://www.youtube.com/watch?v=MZAaeel6c2s[/youtube]
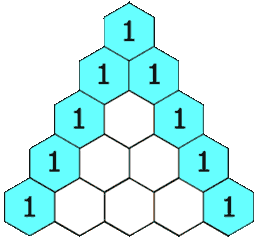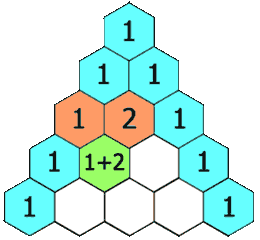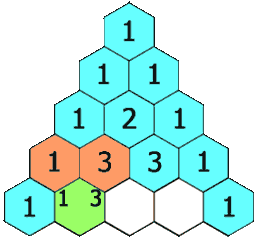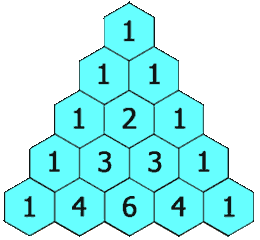
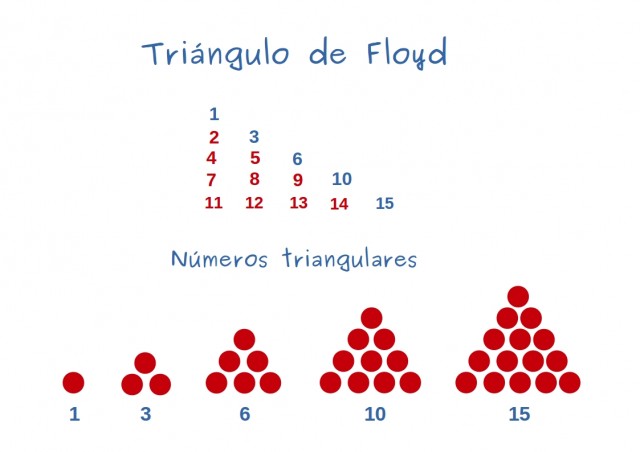
Sin embargo, hay triángulos muy famosos en la historia de la humanidad: unos más ligados al conocimiento, como el triángulo de Pascal, en el que aparecen, entre otras muchos objetos matemáticos, los coeficientes de las distintas potencias de (a+b);
 el triángulo de Floyd, cuya hipotenusa nos da el conjunto de los números triangulares (aquellos que podemos distribuir como un triángulo equilátero);
el triángulo de Floyd, cuya hipotenusa nos da el conjunto de los números triangulares (aquellos que podemos distribuir como un triángulo equilátero);
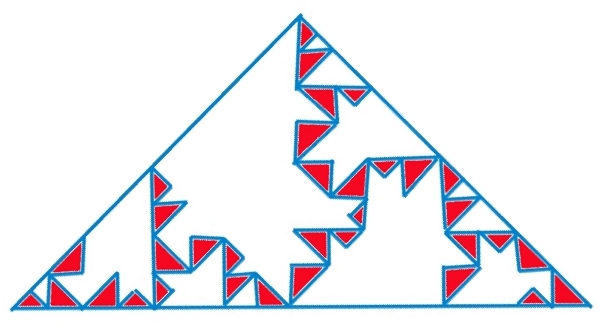
un fractal como el triángulo de Sierpinski;
u otro fractal, también creado a partir de un triángulo, como el fractal de Fibonacci que nos descubrió Mati en esta mateaventura.
Otras veces, el triángulo ha sido vapuleado y desprestigiado apareciendo en mitos y leyendas, como la del triángulo de las Bermudas o, pobre, hasta se le han otorgado propiedades sagradas.
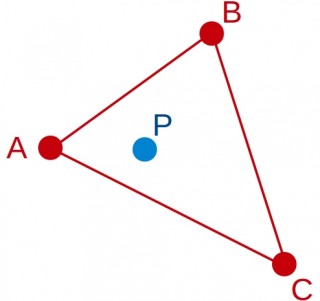
Sin duda, uno de los triángulos más excitantes (para algunos) y más populares en nuestra cultura, es el mal llamado triángulo amoroso. Sí, y digo mal llamado porque normalmente, aunque no siempre, cuando se habla de un triángulo amoroso de lo que se está hablando es de una situación como la siguiente:
Y eso, con todos mis respetos a la geometría clásica, no es un triángulo, sino un grafo, un grafo con un nombre hermoso: .
A poco que lo piensen, encontrarán más moderno decir que están en un amoroso que un triángulo de esas características.
Pero aparte de servir para representar miedos tan irracionales como π, o las fantasías sexuales de alguien, los triángulos se usan con otros fines más asépticos y racionales.
Sí. Los triángulos se usan, por ejemplo, para interpolar y aproximar valores que no conocemos a partir de otros que conocemos, porque los hemos medido, por ejemplo. Huy, lo que he dicho, ¿no?
Vamos a verlo con un ejemplo. Supongamos que hemos medido, usando un taquímetro, la altura en 3 puntos (en rojo en la figura) y queremos conocer la altura de otro punto (el azul) pero sin necesidad de ir de nuevo a medirlo sobre el terreno.
Eso se puede hacer con interpolación baricéntrica. Les cuento cómo.
Si tenemos un triángulo formado por los vértices A, B y C, para cualquier punto de ese triángulo, P, se pueden calcular sus coordenadas baricéntricas respecto de A, B y C. Estas coordenadas baricéntricas serán 3 números, α, β y γ, que suman 1, y que cumplen que (en términos de coordenadas):
P= α.A + β.B + γ.C
Pues bien, si son esas las coordenadas de P en el triángulo y conocemos la altura en A, h(A), en B, h(B) y en C, h(C), podemos dar una aproximación de la altura del terreno en P usando la siguiente fórmula:
h(P)= α.h(A) + β.h(B) + γ.h(C)
Ea, ya tenemos la altura de P sin necesidad de volver al campo a medir, ¿no? Bueno, bueno, seamos prudentes. Para poder fiarnos de esa aproximación de la altura de P hay que comprobar algunas cositas más. Si solo conocemos la altura en 3 puntos (como en nuestro ejemplo) vale, no hay otros triángulos posibles para usar la interpolación, pero si hay más puntos las cosas cambian…
Vamos a fijarnos en el siguiente ejemplo: en ambos casos, hemos medido la altura en los puntos amarillos, usando un taquímetro, y en ambos casos, hemos construido triángulos con vértices en los puntos para los que conocemos su altura, los hemos triangulado, hemos hecho una triangulación de los puntos amarillos.
Fíjense que hemos usado casi los mismos triángulos en los dos ejemplos, salvo en la zona que aparece sombreada.
Si ahora, usando interpolación baricéntrica, queremos saber la altura del punto rojo, observamos que, depende de la triangulación que elijamos, nos da un resultado. Y sí, son muy diferentes. ¿Qué ha pasado aquí?
 El sentido común nos empuja a pensar que la mejor aproximación es la de 985 metros. En el otro caso, si entre 2 puntos a 980 y 990 metros hubiese un punto a una altura de 23 metros, nuestro topógrafo lo hubiese medido, para poder dar una representación más fiel del terreno e indicar la existencia de una depresión. Podemos deducir que si el topógrafo no midió en el punto rojo es porque no encontró nada relevante en esa zona. O porque el topógrafo es muy malo, pero vamos a descartar esta opción.
El sentido común nos empuja a pensar que la mejor aproximación es la de 985 metros. En el otro caso, si entre 2 puntos a 980 y 990 metros hubiese un punto a una altura de 23 metros, nuestro topógrafo lo hubiese medido, para poder dar una representación más fiel del terreno e indicar la existencia de una depresión. Podemos deducir que si el topógrafo no midió en el punto rojo es porque no encontró nada relevante en esa zona. O porque el topógrafo es muy malo, pero vamos a descartar esta opción.
Concluimos, entonces, que la mejor triangulación es la de la izquierda. ¿Qué tiene esta triangulación mejor que la otra? Pues que tiene ángulos más grandes, triángulos más redonditos. Las dos triangulaciones son casi iguales, pero donde no lo son, la triangulación de la izquierda tiene triángulos con ángulos más grandes.
Por lo tanto, para modelizar un terreno digitalmente, ya tenemos el algoritmo. Medimos en algunos puntos, triangulamos bien esos puntos y para el resto, calculamos la altura usando interpolación baricéntrica en el triángulo en el que haya caído. Gráficamente, se puede pensar como que dibujamos los puntos (aquellos en los que medimos) en un plano (nos olvidamos de la 3ª coordenada, la que nos da la altura); triangulamos esos puntos en el plano y por último, los levantamos a la altura que sabemos que tienen, levantando los triángulos a la vez y obteniendo un modelo aproximado del terreno real.
 Muy chulo, ¿no? Lo único chungo es que para podernos fiar de este modelo la triangulación, como hemos dicho antes, tiene que ser buena. De hecho, queremos hacerlo con la mejor triangulación posible en el sentido que hemos dicho, la que tenga mejores (mayores) ángulos, la que tenga los triángulos más redonditos. A esta triangulación se le conoce con el nombre de triangulación de Delaunay.
Muy chulo, ¿no? Lo único chungo es que para podernos fiar de este modelo la triangulación, como hemos dicho antes, tiene que ser buena. De hecho, queremos hacerlo con la mejor triangulación posible en el sentido que hemos dicho, la que tenga mejores (mayores) ángulos, la que tenga los triángulos más redonditos. A esta triangulación se le conoce con el nombre de triangulación de Delaunay.
A primera vista, esto puede agobiar. Pero en matemáticas, como en la vida en general, las cosas que más nos hacen sentir son las que al principio nos cuesta un poco, ¿no? Y digo que puede agobiar porque en un primer acercamiento, uno puede pensar: “¿¿Tengo que calcular todas las triangulaciones distintas posibles y medir los ángulos de todas ellas??” Bueno, tú allá, pero para un conjunto de puntos, aunque no se conoce el número concreto en función del número de puntos, puedes tener una ‘jartá’ de triangulaciones diferentes. Y, para agobiarte un poco más, no olvides que en la práctica, en problemas reales, el conjunto de datos iniciales del que dispondrás, los puntitos donde hemos medido, puede ser también una ‘jartá’ de grande. Pero, don’t panic and keep calm, porque en matemáticas, como en la vida en general, si se miran las cosas con calma, normalmente, no son tan difíciles.
Vamos a pensar un poco, que para eso cargamos sobre nuestro cuello con un kilo y medio de cerebro, más o menos.
Hay unas aristas, segmentos, que están en todas las triangulaciones seguro y, por lo tanto, también estarán en la de Delaunay: las que forman la frontera de la envolvente convexa del conjunto de puntos (la envolvente convexa sería la forma que adoptaría una goma elástica si la soltamos alrededor del conjunto de puntos, en los que hemos puesto, en cada uno, un clavo).
Anda, pues ya tenemos unas pocas de aristas seguras de la triangulación de Delaunay.
Inciso: esta propiedad de las triangulaciones, la de que las aristas de la envolvente convexa del conjunto de puntos, forman parte de cualquier triangulación, debe ser sumamente intuitiva. Lo digo porque cuando mi hijo pequeño tenía 6 años y yo lo ponía a triangular puntos en un papel para que me dejase trabajar, la tercera o cuarta vez, no recuerdo exactamente, lo primero que dibujó fueron esas aristas, las de la envolvente convexa, porque intuyó (supongo) que esas siempre le iban a salir.
Seguimos. Una vez colocadas las aristas de la envolvente convexa, ¿cómo podemos saber si la arista (que no sea de la envolvente) que une a 2 puntos de mi conjunto es una arista buena para la triangulación que estoy buscando, es decir, para la triangulación de Delaunay? Usando un poco de geometría clásica de los tiempos de Thales.
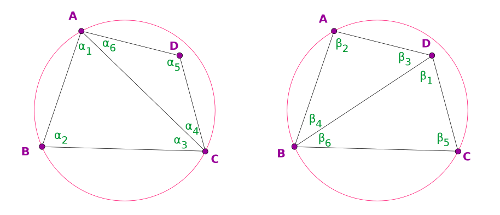
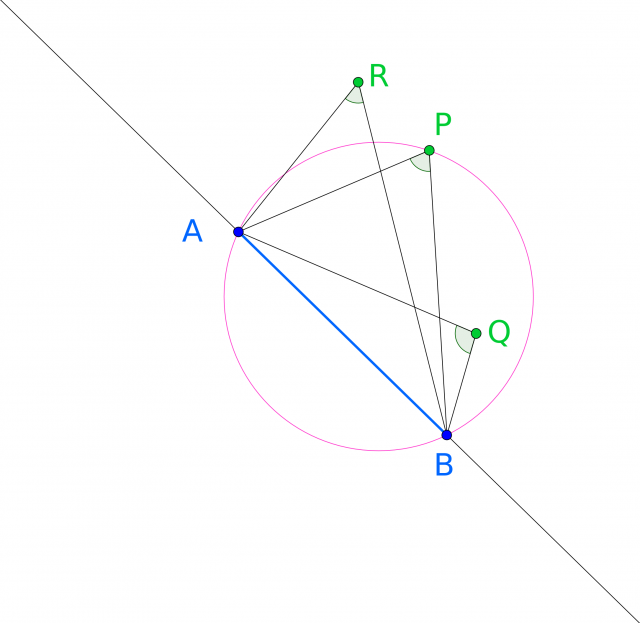
Si A y B son 2 puntos sobre una circunferencia, el segmento que une a dichos puntos se conoce como la cuerda AB. Esta cuerda divide a la circunferencia es 2 arcos de circunferencia. Pues bien, el ángulo con el que cualquier punto de uno de esos arcos ve a la cuerda AB es el mismo.
En la figura siguiente, por ejemplo, el ángulo desde y
es el mismo, y lo sería desde cualquier otro punto del arco marcado en rojo; y también son iguales los ángulos en
y
(y lo sería en cualquier otro punto del arco marcado en verde).
 Más cositas. Cualquier punto interior al círculo, a la derecha de la cuerda AB en nuestra figura anterior, es decir, cualquier punto interior al círculo contenido en el mismo semiplano (de los 2 definidos por la recta AB) que P, ve a la cuerda AB con un ángulo mayor que P. En nuestro dibujo, Q ve a la cuerda AB con más angulo que P. Y también, cualquier punto en el mismo semiplano que P exterior al círculo (como R en nuestro dibujo) ve a la cuerda AB con menor ángulo que P.
Más cositas. Cualquier punto interior al círculo, a la derecha de la cuerda AB en nuestra figura anterior, es decir, cualquier punto interior al círculo contenido en el mismo semiplano (de los 2 definidos por la recta AB) que P, ve a la cuerda AB con un ángulo mayor que P. En nuestro dibujo, Q ve a la cuerda AB con más angulo que P. Y también, cualquier punto en el mismo semiplano que P exterior al círculo (como R en nuestro dibujo) ve a la cuerda AB con menor ángulo que P.
 Esto, como digo, es geometría clásica, de la de toda la vida de Thales. Pero nos sirve para buscar nuestra triangulación de Delaunay.
Esto, como digo, es geometría clásica, de la de toda la vida de Thales. Pero nos sirve para buscar nuestra triangulación de Delaunay.
Recordemos por dónde estábamos. Tenemos un conjunto de puntos (de los que conocemos su altura, por ejemplo) y queríamos calcular la triangulación con mejores ángulos para interpolar, la triangulación de Delaunay. Sabemos ya que las aristas de la envolvente convexa (las de la gomilla y tal) seguro que están y queremos conocer qué otras aristas tenemos que añadir.
¿Cómo lo hacemos? Hacemos un triangulación de los puntos a nuestro antojo, sin preocuparnos de nada, simplemente, añadiendo segmentos (aristas) entre los puntos, de 2 en 2, sin que se crucen con los que ya están dibujados. Cuando no podamos añadir ninguno más, lo que nos queda es una triangulación. Ahora nos fijamos en una arista cualquiera interior (que no sea de las de la envolvente porque esas son de Delaunay, seguro) y vamos a averiguar si dicha arista es de Delaunay.
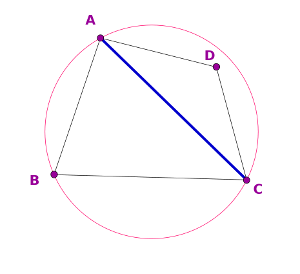
Si la arista es interior, está compartida por 2 triángulos de la triangulación. En la figura siguiente, si nos fijamos en la arista AC, interior, esta es común a los triángulos ABC y ADC.
 Dibujamos el círculo que pasa por los vértices de ABC (es único, 3 puntos no alineados determinan siempre un círculo) y comprobamos si el otro vértice, D (el del otro triángulo) está dentro del círculo.
Dibujamos el círculo que pasa por los vértices de ABC (es único, 3 puntos no alineados determinan siempre un círculo) y comprobamos si el otro vértice, D (el del otro triángulo) está dentro del círculo.
 Si está, como ocurre en nuestro ejemplo, ya sabemos que la arista AC no es de Delaunay, y la tenemos que cambiar por la BD, que es la otra diagonal del cuadrilátero ABCD. Esta operación se conoce como flip, en inglés, y aunque se traduce por giro o intercambio en castellano, lo cierto es que en la comunidad de Geometría Computacional española, le llamamos flip e incluso conjugamos el verbo flipar. Somos así, no hay más.
Si está, como ocurre en nuestro ejemplo, ya sabemos que la arista AC no es de Delaunay, y la tenemos que cambiar por la BD, que es la otra diagonal del cuadrilátero ABCD. Esta operación se conoce como flip, en inglés, y aunque se traduce por giro o intercambio en castellano, lo cierto es que en la comunidad de Geometría Computacional española, le llamamos flip e incluso conjugamos el verbo flipar. Somos así, no hay más.
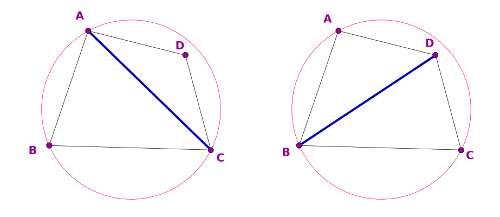 ¿Por qué es mejor BD que AC? Pues porque los ángulos implicados en la triangulación del cuadrilátero ABCD usando esa diagonal, la BD, son mejores (para lo que queremos nosotros) que los resultantes al usar la diagonal AC. Vamos a verlo usando la geometría clásica que hemos visto.
¿Por qué es mejor BD que AC? Pues porque los ángulos implicados en la triangulación del cuadrilátero ABCD usando esa diagonal, la BD, son mejores (para lo que queremos nosotros) que los resultantes al usar la diagonal AC. Vamos a verlo usando la geometría clásica que hemos visto.
Lo que tenemos que ver es que el ángulo más pequeño de la triangulación con la diagonal BD es mayor que el ángulo más pequeño de la triangulación con AC. Es decir, que el ángulo más pequeño del conjunto es más grande que el ángulo más pequeño del conjunto
. Dicho de otra manera, que el ángulo más pequeño del conjunto
es uno de los α.
Si nos fijamos en el segmento CD, el punto B, es interior al círculo definido por ACD, por lo tanto, como hemos visto hace unas líneas, el ángulo con el que B ve a CD es mayor que el ángulo con el que lo ve A. Esto es .
De la misma manera, si nos fijamos en el segmento BC, como D es interior al círculo ABC, tenemos que el ángulo en D es mayor que el ángulo en A y que, por lo tanto, .
 Usando razonamientos similares, tenemos que
Usando razonamientos similares, tenemos que (usando el segmento AB) y
(usando el segmento AD).
Y, claramente, y
. Por lo tanto, el menor ángulo de
no puede ser un β porque para todos hay un α menor. Con esto tenemos que la arista BD es mejor que la AC en el cuadrilátero ABCD.
Pero este mismo razonamiento nos sirve para cualquier arista interior, que no sea de la envolvente: para que sea de Delaunay, tenemos que comprobar que los 2 círculos circunscritos a los 2 triángulos pegados por dicha arista, no contienen a ningún otro punto.
Si uno de dichos círculos no esta vacío, tenemos que hacer flip.
Este criterio, el del círculo vacío, nos permite diseñar algoritmos para calcular la triangulación de Delaunay de un conjunto de puntos, sin necesidad de probar con todas las triangulaciones posibles y quedarnos con la de mejor ángulo.
Pero si hay por aquí algún amigo de Voronoi, le voy a contar una forma también muy rápida de conseguir la triangulación de Delaunay. Para nuestro conjunto de puntos calculamos, como ya vimos, el diagrama de Voronoi
 A continuación, unimos cada punto con todos sus vecinos de Voronoi, esto es, con todos los puntos que comparten la frontera de su región de Voronoi con él.
A continuación, unimos cada punto con todos sus vecinos de Voronoi, esto es, con todos los puntos que comparten la frontera de su región de Voronoi con él.
Si lo hacemos con todos, nos queda:
Si borramos ahora el diagrama de Voronoi, miren lo que nos queda:
Efectivamente, es una triangulación, pero no una triangulación cualquiera, no, hija, no, es la triangulación de Delaunay, y se puede comprobar viendo que los círculos asociados a cada triángulo no contienen a ningún otro punto del conjunto inicial. Aquí hemos dibujado 3 de ellos:
No me digan que no es sumamente maravilloso.
Pero aún hay más cosas, si queremos saber cuáĺes son los 2 puntos más cercanos del conjunto, solo tenemos que medir las aristas de Delaunay y quedarnos con la más corta, ¡no es necesario calcular todas las distancias!
O por ejemplo, imaginen que quieren construir un servicio incómodo (vertedero, central nuclear, granja de pollos, un McDonalds…) y lo quieren hacer lo más alejado posible de los núcleos urbanos (representados por puntos) para no molestar, pero sin salirse de la envolvente convexa (no vale mandarlo al país vecino), ¿dónde lo colocan? Ajá, en el centro del mayor círculo circunscrito a los triángulos de Delaunay del conjunto. En la figura siguiente, si los puntos verdes representan a los núcleos urbanos, habría que colocar el servicio incómodo en el punto rojo, que es el centro del mayor círculo circunscrito en un triangulo de Delaunay que se queda dentro de la envolvente.
Si es que, los triángulos son muy apañaos… Y no solo para modelar digitalmente terrenos, sino para un montón de aplicaciones más que os iremos contando por aquí, o por nuestro blog de Mati.

Nota final y ejercicio propuesto:
He usado GeoGebra para hacer algunos de los dibujos de este artículo y, ¡oh, sorpresa! He descubierto que no siempre GeoGebra calcula bien la triangulación de Delaunay…
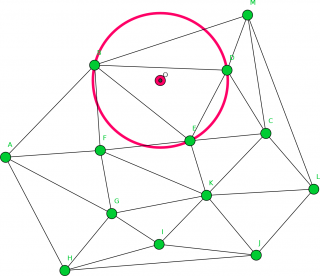
Fíjense en la triangulación de Delaunay que me dibujó Geogebra para este conjunto de puntos:
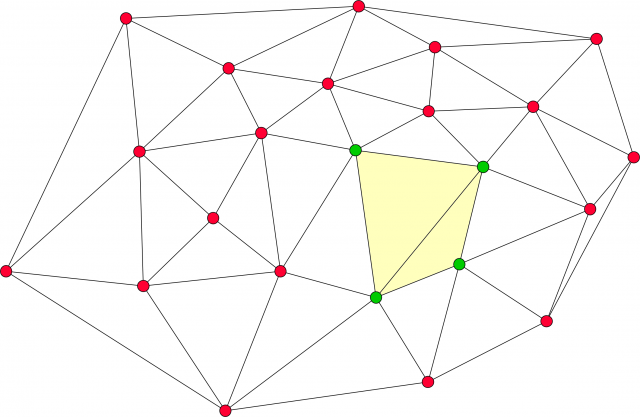
 Ahora, fíjense, por ejemplo, en la triangulación del cuadrilátero formado por los 4 puntos destacados en verde.
Ahora, fíjense, por ejemplo, en la triangulación del cuadrilátero formado por los 4 puntos destacados en verde.
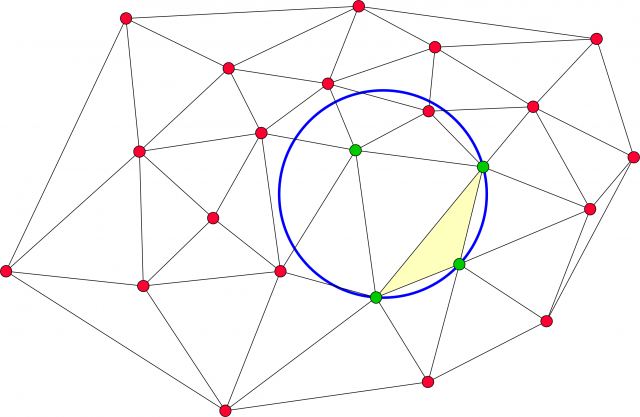
Efectivamente, no son triángulos de Delaunay. Si dibujan el círculo circunscrito al triángulo más a la derecha, no está vacío.
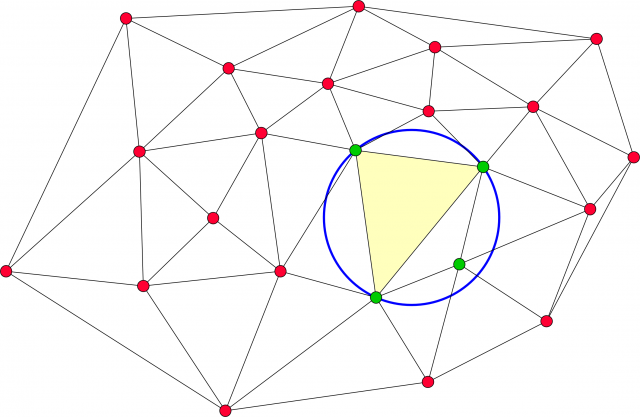 Y tampoco lo está el círculo circunscrito al otro triángulo.
Y tampoco lo está el círculo circunscrito al otro triángulo.
Bueno, estoy segura de que corregirán este fallo pronto y podremos seguir usando esta herramienta, GeoGebra con tranquilidad. Si no la conocen, se la recomiendo.
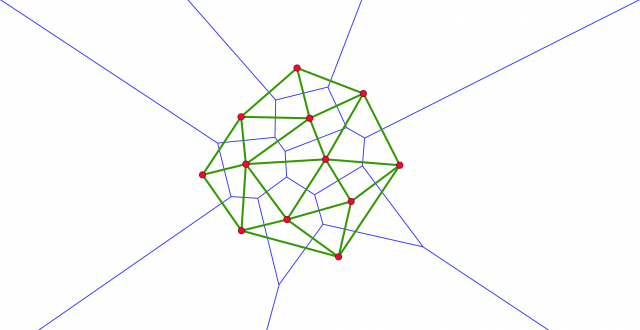
Mientras lo arreglan, les dejo una triangulación que GeoGebra me dio como Delaunay que no lo es, a ver si detectan el/los fallos. Les he dejado dibujado también el diagrama de Voronoi para que les resulte más fácil detectar el error.
Hasta pronto y ¡no olviden supermineralizarse y supertriangularse! 😉
Más información en el libro de Preparata y Shamos o en este otro de de Berg y otros, por cierto, muy interesante como primer acercamiento a la Geometría Computacional.
Soy profesora del área de Matemática Aplicada de la Universidad de Sevilla desde un maravilloso día soleado de Noviembre de 1995. Desde entonces he descubierto que la satisfacción de investigar es sólo comparable a la de contar y enseñar lo que has descubierto. Durante más de 10 años esto último se redujo al ámbito de mis clases en la Universidad y a las comunicaciones en congresos. Con la llegada de mis enanos se me planteó el reto de contarlo fuera del aula, en la alfombra del salón. Y oye, me gustó. Ahora dedico parte de mi tiempo libre a la divulgación, para niños de 9 a 99 años, consciente de que a todo el mundo le gustan las matemáticas, solo que algunos aún no lo saben. Mis coordenadas en: claragrima.com.