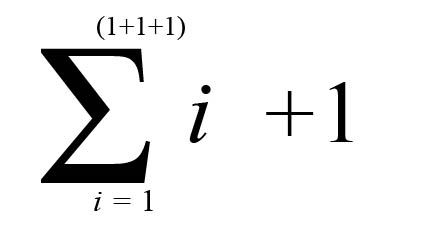Este es un problema simple y divertido; es un poco viejo pero siempre existe la posibilidad de que usted, amable lector, no lo haya visto antes.
El problema es como sigue: tenemos a nuestra disposición cinco 1’s, que podemos usar de cualquier forma que creamos conveniente. Con estas cinco unidades, debemos construir los números del 1 al 10, y podemos usar los signos matemáticos de las operaciones que queramos (suma, resta, raíz cuadrada, etc. ), pero no podemos usar ningún otro número. Para usar el 0, tenemos que poner (1-1); para hacer un exponente al cuadrado, ponemos (1+1). Pero sí podemos juntarlos como 11, 111, etc.
Por ejemplo: 1 x 1 x 1 x 1 x 1 = 1,
o bien: (1 + 1) / (1 + 1) x 1 = 1,
y también: (11/11) x 1 = 1.
En todos estos ejemplos estoy usando un extra 1 (el lado derecho de la igualdad) simplemente para demostrar que la operación es válida. Ahora bien, del 1 al 5 las respuestas inmediatas son triviales, porque los cinco números pueden ser construidos usando únicamente suma y multiplicación. Por supuesto, puede intentar construirlos de formas más imaginativas, por ejemplo:
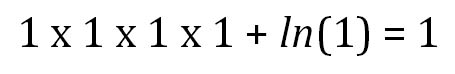 (El logaritmo natural de 1 es 0).
(El logaritmo natural de 1 es 0).
O bien: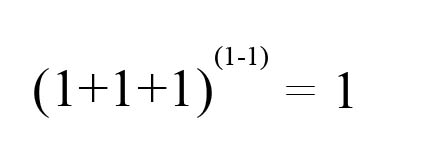 (Cualquier número elevado a la potencia 0 es 1).
(Cualquier número elevado a la potencia 0 es 1).
Si de plano se quiere poner muy exótico y usar notación de teoría de conjuntos, puede hacer algo como:
Aunque ahí la verdad me estoy pasando un poco. Pero puede intentar hacer algo más decente que eso. Y si es usted un friki total, puede considerar operaciones incluyendo notación hexadecimal:
 (El 10 en notación hexadecimal se escribe Ahex ).
(El 10 en notación hexadecimal se escribe Ahex ).
Así se puede pasar un buen rato tan sólo con el 1, pero le diré que si seguimos solamente con operaciones sencillas, las cosas son más interesantes del 8 al 10, porque necesariamente hay que usar exponentes y agrupaciones con paréntesis. Sin embargo siguen siendo muy simples de encontrar. Inténtelo y verá que no tarda mucho.
Pero claro, de eso no se trata el test. Del 1 al 10, el número 7 es la excepción: hay que pensar un poco más para encontrarlo porque la forma de construirlo no es tan inmediatamente aparente como las de sus nueve colegas.
Más abajo voy a poner tres formas distintas de llegar al 7 usando los mencionados cinco 1’s, ordenadas de menos a más creatividad, pero tómese un rato para ver si puede encontrar soluciones antes de verlas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Soluciones:
El problema puede ser encontrar una expresión para la operación 10-3. Aquí está una forma de hacerlo:
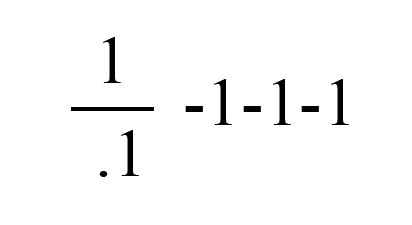 Aquí hay una segunda solución, más creativa, que lo que hace es encontrar 6+1:
Aquí hay una segunda solución, más creativa, que lo que hace es encontrar 6+1:
Que quiere decir “la sumatoria de todos los valores de i, donde i va desde 1 hasta 3, más 1”.
Y finalmente una manera más creativa todavía:
 No se enoje con esta última. Lea de nuevo las reglas y verá que es válida.
No se enoje con esta última. Lea de nuevo las reglas y verá que es válida.
Referencias:
List of logic symbols. Wikipedia.
Hexadecimal. Wikipedia.
Nací en México y vivo en China desde el 2000, donde estudié idioma e historia, y luego fui investigador visitante en el Centro Internacional Wan Lin Jiang de Economía y Finanzas, así como profesor de economía e historia para extranjeros en la Universidad de Zhejiang. Actualmente dirijo el Mexico-China Center y doy conferencias acerca de ciencia y cooperación tecnológica internacional.