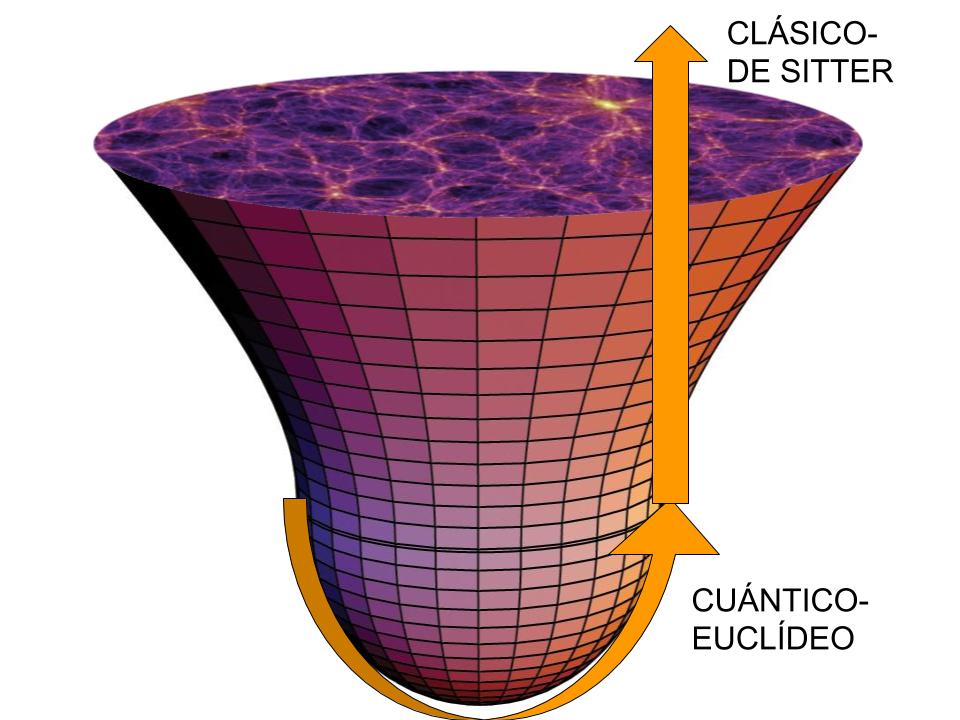
Seguimos en nuestro camino para entender el último trabajo de Stephen Hawking.
Ya hemos pasado por una revisión del universo inflacionario y de aquello de las dualidades y el principio holográfico. Estos son ingredientes esenciales para llegar a vislumbrar de qué va el artículo que nos ocupa. Hoy vamos a por otro de esos ingredientes.
En esta entrada nos vamos a centrar en un aspecto muy interesante, el proceso de origen del universo en sí mismo. La teoría cosmológica, la estándar o inflacionaria, nos explican cómo evoluciona nuestro universo pero no explican de dónde sale el universo ni qué proceso lo hace posible. Stephen Hawking, junto a sus colaboradores James Hartle y Thomas Hertog, han desarrollado una propuesta que explicaría justamente eso… el origen del universo. La propuesta es conocida como Propuesta de la Ausencia de Frontera.
Pasen y lean.
Singularidades cosmológicas

A principios de la década de los 70 del pasado siglo, Stephen Hawking, junto a Roger Penrose, probó que si tenemos solo en cuenta la Relatividad General (o cualquier teoría geométrica del espaciotiempo como explicación de la gravedad en la que se cumple que la gravedad es atractiva, no hay posibilidad de viajar en el tiempo y se forman regiones muy pequeñas con altas concentraciones de energía) la teoría te dice que en el origen del universo hay una singularidad.
Ojo, la singularidad la tiene la teoría, la singularidad no es algo físico sino que es un artefacto que surge en la teoría al intentar aplicarla a situaciones para las que no puede darnos respuesta. Que al aplicar la relatividad general al universo (de bolsillo) nos diga que hay una singularidad en su origen lo que quiere decir es que no podemos aplicar la relatividad general a ese suceso físico.
Sin embargo, hoy día pensamos que para acometer el estudio del propio origen del universo así como su evolución temprana hemos de emplear simultáneamente las técnicas de la gravedad y de la cuántica. Por ello, se hace necesaria una teoría cuántica de la gravitación para poder dar respuesta a esas interrogantes. Por desgracia, aún hoy no tenemos un modelo de gravedad cuántica plenamente satisfactorio. Sí, lo sé, hay opciones como la teoría de cuerdas o la loop quantum gravity que pueden intentar dar respuesta a este tema. Sin duda alguna, estos estudios son muy interesantes pero aún hoy no podemos saber si son acertados o no. Y claro, cuando tengamos una teoría final de la cosmología cuántica seguro que hay qué explicar qué papel juega en ella la propuesta de Hawking y colaboradores.
Así que Hawking, en 1983, junto a James Hartle tomó el siguiente punto de vista:
Si el universo en su origen es cuántico, entonces hemos de ser capaces de dar el estado cuántico de todo el universo al completo.
El artículo inicial de este tema lo podéis encontrar aquí:
La cuántica
La mecánica cuántica es una de las grandes conquistas intelectuales de la humanidad. Que hayamos entendido que la naturaleza, en su nivel más básico, se comporta tal y como dicta la mecánica cuántica (aún no hemos podido encontrar ninguna falla entre la teoría, sus predicciones y los experimentos) es un acto sublime de inteligencia. La cuántica nos es ciertamente extraña porque sus efectos y sus características se muestran en condiciones muy alejadas de nuestra experiencia cotidiana. Esto no quiere decir que la cuántica no sea importante en nuestra escala sino que los fenómenos en dicha escala se combinan de tal forma que nos da la impresión de que la física es justamente como la que podemos percibir. Sin embargo hay que insistir en que la física, en última instancia y por lo que sabemos hoy día, es puramente cuántica.
En cuántica tenemos tres elementos esenciales, discretización, superposición y entrelazamiento. Para un breve resumen de estas características podéis echarle un ojo a este vídeo:
Sin embargo, lo que nos interesa aquí es lo siguiente:
Los sistemas físicos no han de tener necesariamente valores definidos de las distintas magnitudes físicas. Por ejemplo, un sistema no ha de tener una energía definida, o una posición definida o un momento lineal (análogo a la velocidad en situaciones usuales) definido. Cuando ocurre esto, la cuántica nos dice que dado un sistema puede tener un conjunto de valores de dichas magnitudes y con qué probabilidad encontraremos cada uno de los valores posibles al efectuar la medida de la magnitud correspondiente sobre el sistema en cuestión.
Además de esto, como subproducto, podemos asegurar que hay pares de magnitudes en las que si conocemos el valor de una de ellas la otra está totalmente indeterminada. Eso es lo que nos dice el principio de indeterminación de Heisenberg. El ejemplo más socorrido es el que liga en una relación de indeterminación la posición y el momento de un sistema. Si conocemos uno el otro estará totalmente indeterminado. ¿Es eso una falta de finura experimental? No, es una característica esencial de la naturaleza en el nivel cuántico. Es que dichas magnitudes, las involucradas en relaciones de indeterminación, no tienen valores definidos simultáneamente en los sistemas.
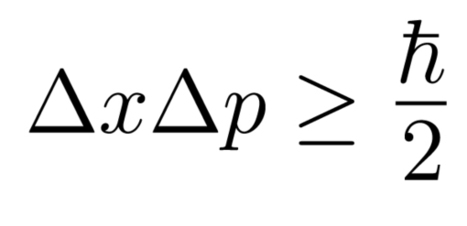
Ahora bien, imaginemos que queremos describir el proceso en el que un sistema físico se traslada desde el punto A al punto B. Para que quede claro:
Esta imagen es un claro ejemplo de lo que se conoce como imagen inútil en una entrada. Pero no nos perdamos en los detalles. Sigamos.
Desde el punto de vista clásico, para resolver el movimiento desde A hasta B, lo que hacemos es plantear las ecuaciones de movimiento del sistema bajo estudio que vendrán determinadas entre otras cosas por la interacción que hace que el sistema se mueva. El caso es que cuando resolvermos las ecuaciones de movimiento en realidad lo que encontramos es una familia de soluciones, una familia de posibles caminos entre A y B.
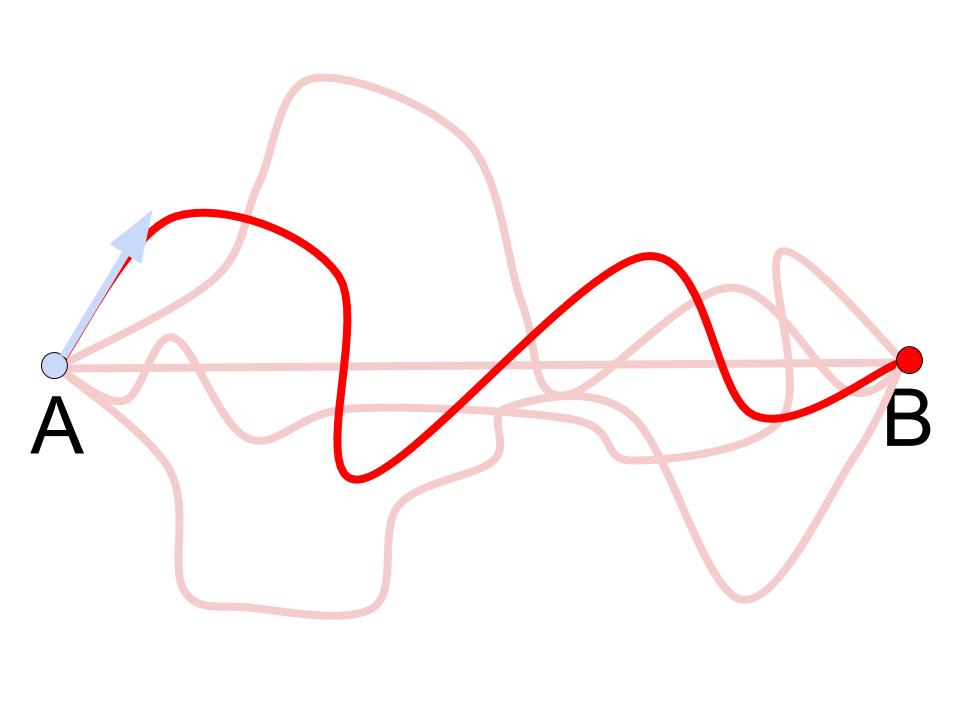
Ahora bien, ¿Cómo sabemos cuál de todas las posibles trayectorias es la que se realiza físicamente? (Ten en cuenta que tendría que haber dibujado infinitas trayectoras posibles, pero me he cansado, espero que captes la idea) La respuesta es maravillosamente fácil. Basta con saber la posición inicial y la velocidad inicial. Con esos dos datos podemos seleccionar la curva física que realiza el sistema en su movimiento de A a B. (También vale para cualquier par de ha pasado por este punto en este instante y con esta velocidad).
Así pues, podemos conocer, si tenemos en nuestro poder las fórmulas de las interacciones en juego en el problema en cuestión y las condiciones iniciales de posiciones y velocidades el camino recorrido por el sistema bajo estudio. Fácil y sencillo.
Ahora bien, en cuántica tenemos un problema. No podemos idenficar trayectorias porque, como hemos discutido, es imposible dar a la vez los valores de la posición y el momento en cada instante de tiempo. Simplemente no están definidos. Por lo tanto, lo único que sabemos desde el punto de vista cuántico es que el sistema sale de A (porque lo hemos preparado ahí) y queremos conocer la probabilidad de que llegue a B cuando pase un determinado intervalo de tiempo.
Así que hemos de prescindir de trayectorias y la cuántica se fundamenta, en su versión más estándar, en un formalismo matemático que no hace uso de dichas trayectorias. Eso sí, nos da las probabilidades de que un sistema salga de A y llegue a B sometido a tal o cual interacción. La cuántica nos permite calcular unas cosas denominadas amplitudes cuyos cuadrados nos dan las probabilidades de que ocurra tal o cual cosa:
Toda esta historia tiene un giro fantástico un giro que fue posible gracias al ingenio y el genio de Richard Feynman.
Integrales de Camino = Suma de Historias
Como hemos dicho, las particularidades de la cuántica se pueden relacionar con eso de que los sistemas no tienen perfectamente definidas todas sus propiedades físicas sino que estas están indeterminadas. No es que no podamos extraer a la vez un par de magnitudes que verifiquen una relación de indeterminación porque seamos torpes experimentalmente hablando. La cuántica establece que dichas magnitudes no están definidas en un sistema simultáneamente.
En los ejemplos anteriores la cuántica nos da la forma de calcular la probabilidad de que un sistema, pongamos por caso una partícula, salga del punto A y llegue al punto B transcurrido un intervalo de tiempo prefijado. Así, la cuántica la podemos formular sin recurrir a trayectorias, claro está, como no se pueden conocer posiciones y momentos (velocidades) a la vez pues no usamos trayectorias y listo. Pero esa no es la única opción…
Vamos a ver, hay dos formas de restringir el uso de información. La primera forma es aquella en la que eliminamos toda posibilidad de acceso a la misma, lo que se llama usualmente censura. La segunda forma es más sutil pero igualmente efectiva. Si no queremos que alguien acceda a una determinada información es muy útil proporcionarle toda la información disponible a la vez, esto es lo que usualmente llamamos internet. La opción de Feynman para formular la cuántica es la análoga a este segundo caso. Dado que no podemos definir trayectorias para saber el camino que siguen los sistemas cuánticos…. ¡Digamos que va por todos los caminos posibles!
Es decir, que para decidir la probabilidad de que una partícula salga de A y llegue a B en un intervalo de tiempo tendremos que considerar simultáneamente todas las posibles formas de conectar A con B.
Evidentemente ese no es el final de la historia. Para poder utilizar esta idea lo que hemos de tener, y es lo que Feynman introdujo, es cuánto aporta cada trayectoria posible a la amplitud de probabilidad (ya sabéis, eso que hemos de elevar al cuadrado para obtener la verdadera probabilidad de que ocurra algo). La amplitud total para el proceso de ir de A a B será la suma de las amplitudes asociadas a cada una de las posibles trayectorias por raras que sean. Dado que hay infinitas posibilidades de trayectorias y pueden estar las unas de las otras tan cerca como queramos la suma se transforma en una integral.
Tal vez sea bueno ver la estructura (no es la más exacta pero nos hacemos una idea) de cómo luce una integral de camino de estas:
Lo que caracteriza cada trayectoria y lo que nos permite asignarle una amplitud es esa S en esa fórmula. Eso tiene un nombre, se llama la acción y es algo que se calcula a partir de la energía cinética y potencial del sistema. Cuando el sistema recorre una trayectoria dada esa acción es un número asociado a la misma.
Con esta receta recuperamos todos los hechos relevantes de la cuántica. Así que esta es una forma la mar de buena de pensar en términos cuánticos.
Lo clásico desde lo cuántico
Un aspecto interesantísimo de estas integrales de camino es que nos dan una explicación entendible del hecho de que en nuestro nivel sí podamos hablar en términos de trayectorias definidas. El problema radica en que si la naturaleza es cuántica, ¿cómo es que nosotros no percibimos hechos cuánticos en nuestra vida cotidiana?
La razón estriba en que el comportamiento clásico emerge, desde el punto de vista de las integrales de Feynman, siempre y cuando una de esas trayectorias tenga un valor extremo de la S, la acción. Es decir, cuando hay una trayectoria (o conjuntos de trayectorias muy parecidas entre sí) cuyo valor de la acción le gana a todas las demás. Entonces en la suma de todas las trayectorias es justamente la de valor extremo la que más contribuye a dicha suma. Así que el grueso de la probabilidad vendrá de esa trayectoria que es la que identificaríamos en un contexto clásico como el que observamos en nuestra vida diaria.
Nota para expertísimos: Sí, sí, en realidad es porque el valor de la acción extremal hace que tenga una contribución constructiva en la interferencia cuántica de todas las posibilidades y el resto, que dan contribuciones altamente oscilantes, se cancelan entre sí. Pero no nos pongamos demasiado finos.
Lo de Feynman para Universos
La idea de Hawking y Hartle, que ya hemos comentado al principio de esta entrada, es que el universo en su conjunto ha de venir descrito por una amplitud de probabilidad cuántica. Esa amplitud de probabilidad recibe el nombre de función de onda. Por lo tanto, debería de ser posible hablar de la función de onda del universo. Esa función de onda describiría un universo completo y nos daría la probabilidad de que dicho universo existiera.
Lo ideal sería tener una teoría que nos permitiera calcular dicha función de onda. Desgraciadamente para hacer eso deberíamos de tener una teoría de gravedad cuántica que aún no está disponible en su forma última (aunque se está trabajando muy duramente en ello, aproximadamente llevamos 120 con la tarea). Por lo tanto, Hawking y Hartle idearon una forma de construir esa función de onda a partir de distintos argumentos que pueden ser más o menos factibles y dejar para luego dos cuestiones importantes:
- Saber si la función de onda propuesta predice cosas relevantes para nuestro universo.
- Saber si esa función de onda del universo propuesta puede derivarse de una teoría de la gravedad cuántica.
Por ahora, lo que se puede hacer es proponer la función de onda del universo e intentar extraer las predicciones sobre el universo a partir de ella. El segundo punto, como hemos indicado, deberá de esperar un poco más por el momento.
Si miramos nuestra imagen del origen del universo nos topamos con un problema:

Si suponemos que el universo tuvo un origen entonces su vida es finita. El problema estriba en que según la relatividad general el punto del origen es una singularidad de la teoría por lo que la relatividad general no nos puede decir nada sobre el proceso preciso y precioso de la creación. Lo que esto significa, permítanme que insista, es que necesitamos incorporar los fenómenos cuánticos para poder decir algo con sentido sobre la creación del universo. Aquí es donde es bueno tener una función de onda cuántica del universo al completo.
Hawking y Hartle construyeron dicha función de onda del universo siguiendo estos pasos:
- Quisieron usar la formulación cuántica de Feynman aplicada a todo el universo. En la discusión anterior hemos visto que para estudiar la probabilidad de que una partícula cuántica vaya del punto A al punto B hemos de conocer esos puntos y el instante en el que son ocupados por la partícula. Para el universo, lo que tenemos es que sabemos como es el universo hoy.

- En nuestro universo tenemos cosas, campos/partículas físicos, que representaremos por [E] y tenemos una forma de medir distancias en el espacio, que representaremos por [h]. Por tanto, la configuración de nuestro universo hoy matemáticamente vendrá dada por la determinación de [h,E].
- Además, sabemos que nuestro universo tuvo un origen, pero este origen no puede ser singular. Aquí es donde está el problema. Lo que necesitamos es que el origen del universo sea algo regular. Geométricamente hablando, recordemos que la gravedad según las teorías actuales está relacionada con la geometría del espaciotiempo, el espacio no ha de tener un punto singular sino que tiene que ser regular en toda su evolución.
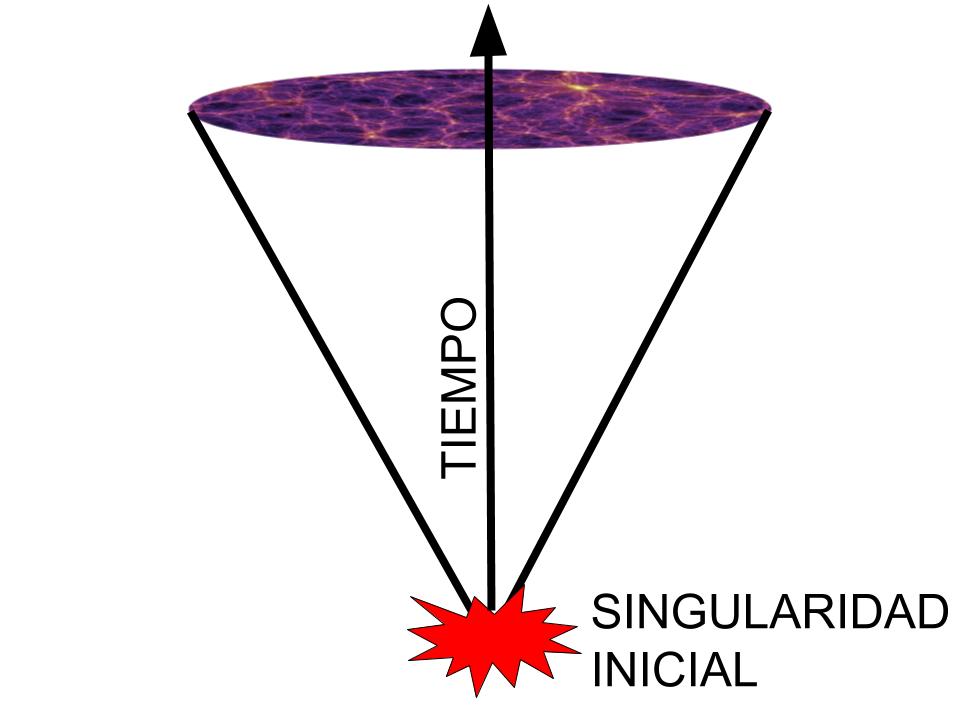
- Afortunadamente, la matemática nos permite describir situaciones en las que la geometría completa emerge de forma regular sin puntos singulares. Para entender esto pensemos en lo siguiente:
En esta situación tenemos un punto del que no podemos decir nada. Es un punto en el que el espacio y el tiempo dejan de tener sentido porque nuestra teoría sobre el espacio y el tiempo, la relatividad general, no puede decirnos nada acerca de dicho punto.
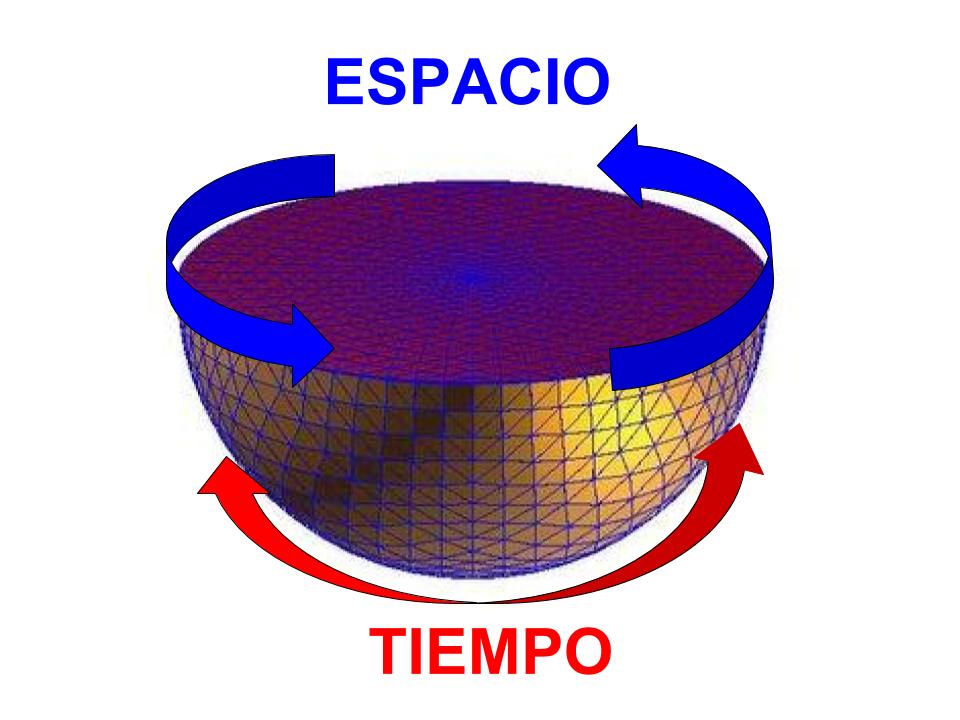
Por fortuna, podemos recurrir a un truco matemático, podemos ir a situaciones en las que en el inicio tanto el espacio como el tiempo se comportan exactamente de la misma manera. Es decir, igual que podemos ir de arriba a abajo, de derecha a izquierda, etc, en el espacio, podemos pensar situaciones en las que en el tiempo podamos de ir hacia adelante y hacia atrás en el mismo. Es decir, espacio y tiempo tienen el mismo carácter. Por ejemplo, así:
Esto nos puede parecer totalmente raro, lo es, pero está permitido siempre que estemos en un régimen cuántico. De hecho, para los expertos y expertas, esto es tomar en la integral de camino una rotación de Wick (generalizada) que nos lleva a un régimen Euclídeo donde el espacio y el tiempo tienen el mismo carácter. Sí, sí, no está muy claro si esto ayuda o no con la cosmología cuántica pero por el momento es lo que hay. Volviendo a las personas normales como el que escribe y los que leen, si hemos leído todos los libros de Hawking y nos hemos perdido cuando habla de tiempo imaginario… a esto es a lo que se refiere. Si ahora nos preguntan cuál es el primer instante de tiempo en ese espacio que está dibujado simplemente no lo podemos decir, todos los puntos de la semiesfera (o puedes pensar en una esfera completa) son iguales a ese respecto, no podemos identificar un origen.
Una vez dicho esto, ya estamos en disposición de intentar construir la función de onda del universo a la Hartle-Hawking. Para ello, lo que hemos de hacer es tomar los siguientes datos:
1. Que nuestro universo sea como es ahora — Esto nos dará una condición de llegada del universo (El punto B en el ejemplo anterior con partículas que van de un sitio a otro).
2. Que nuestro universo haya tenido una evolución regular — Esto nos da una condición de salida del universo (El punto A en el ejemplo anterior con partículas que van de un sitio a otro).
Ahora solo tenemos que tener en cuenta todas las formas de pasar de la situación de salida a la situación de llegada (condiciones de contorno del problema) y calcular su amplitud de probabilidad. Esto lo calcularemos construyendo una S, una acción, que contenga todas las formas de medir en el espaciotiempo (métricas) que sean siempre regulares y que tengan en el día de hoy las formas de medir que sabemos que operan en nuestro universo y, por supuesto, todos los campos de forma que hoy tomen los valores que los campos tienen en nuestro universo.
Así luce esta función de onda:
Lo que Hawking y Hartle conjeturaron, con muy buenos argumentos, es que para acabar con un universo como el que vemos hoy hemos de considerar que la mayor contribución a todas esas historias del universo vienen de la mano de universos que evolucionan de esta forma:
Es decir, universos que son regulares siempre y que pasan de un régimen cuántico en el que espacio y tiempo tienen el mismo carácter pero se da una transición en el que el espacio se abre y el espacio se expande tal y como lo hace nuestro universo.
El nómbre de propuesta de ausencia de frontera/contorno viene porque en el origen no hay una frontera clara en la que podamos decir que empieza el tiempo como hemos discutido antes.
La sorpresa
Tal vez te preguntes cómo se pasa de la parte de abajo en la que espacio y tiempo tienen el mismo carácter a un universo que se expande espacialmente en el tiempo y este último avanza solo en un sentido (indicado por la expansión del universo). Se decir, cómo se pasa de la copa semiesférica, que llamaremos parte euclídea, a la parte superior que se comporta como un universo de Sitter (asintóticamente) tal y como lo hace el nuestro.
Si te preguntas eso tal vez disfrutes con la respuesta:
Pue sí, resulta que si asumimos que la descripción dada por la función de onda del universo a la Hartle-Hawking, el universo ha debido de pasar por una época inflacionaria que es la que hace que se pase del régimen euclídeo al régimen de Sitter (asintóticamente). Esa es una maravillosa noticia porque lo que nos dice es que el modelo predice la inflación como algo que ha de ocurrir y no como algo que inventamos nosotros para solventar problemas de la cosmología estándar no inflacionaria.
Hasta aquí la entrada sobre esta hipótesis. En la próxima entrada de la serie ahondamos más en ella y explicamos qué es lo que realmente nos dice el último trabajo de Hawking.
Y no te pierdas la siguiente entrada en la que, con los ingredientes que hemos adquirido en las tres entradas anteriores de la serie, nos adentraremos en el artículo sobre la salida suave a la inflación.
Nos seguimos leyendo…
Intento escribir sobre física. A veces lo he conseguido.
Me parece importante remarcar que creo en cosas que no he visto, por ejemplo, en los electrones. También tengo varios diplomas, del que más orgulloso me siento es el de participante en la Olimpiada Infantil de 1992; nos dieron un bocata de salchichón y una camiseta.