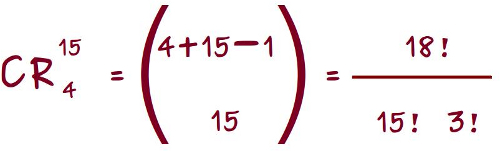Nos mudamos, dejamos Amazings.es y nos vamos a Naukas.com.
Y como siempre que hay mudanza, se plantea el problema de empaquetar las cosas de manera eficiente, optimizando en la medida de lo posible el número de cajas… Huy, esto me recuerda a un problema de Matemáticas, fíjate… Os lo voy a contar, claro, no os voy a dejar intrigados.
Supongamos queremos guardar todos los objetos en cajas para su transporte, naturalmente, estamos en crisis y queremos usar el menor número de cajas posibles (por imposición de la empresa de transporte todas las cajas son del mismo tamaño, para evitarse ellos el problema con el que nos vamos a enfrentar enseguida nosotros). El problema es simple ¿cuántas cajas necesitamos? O mejor dicho ¿se puede diseñar un método que nos garantice que podamos conseguir siempre el mínimo número de cajas? Entiendo por método un algoritmo que corriendo en un ordenador y dándole como dato las dimensiones de todos los objetos. Para simplificar podemos suponer que todos los objetos a empaquetar son rectangulares, prismas rectangulares.
En seguida se nos ocurren dos cosas. Lo primero: no parece tan difícil, voy metiendo objetos en una caja hasta que no quepan más, entonces cierro dicha caja y me dispongo a llenar la segunda.
Lo segundo: si, además, cuento con la ayuda de un ordenador entonces debe ser pan comido.
La pega de la primera estrategia que acabamos de proponer (llenar la primera caja, etc.) es la siguiente… Venga, va, os lo cuento con una simplificación: tenemos una serie de números y queremos agruparlos de tal forma que cada grupo no sume más que una cierta cantidad (mayor que todos los números) prefijada. Si nos fijamos el nuevo problema que acabamos de proponer no es más que la versión 1-dimensional del problema original y, por tanto, es realmente una simplificación (los números son nuestros objetos y la cantidad que no queremos superar son las cajas de la empresa de transporte).
Consideremos el siguiente ejemplo de este problema más simple: Tenemos los números 12, 11, 7,10, 8, 5, 5, 6, 7, 5, 5, 5, 5 y 4 y queremos hacer grupos que sumen 25 o menos.
Empezamos con nuestra estrategia, o sea, metiendo objetos tal como los voy encontrando y hasta que no quepan más en la caja: ponemos 12 en el primer grupo , como 11 también cabe, lo ponemos en el primer grupo y no cabe nadie más. El segundo grupo lo formarán 7, 10 y 8 que estará completo, el tercero 5, 5, 6 y 7 y el cuarto 5, 5, 5, 5 y 4 ¿podíamos haberlo hecho mejor?
Es fácil comprobar ya que la suma de todos los números anteriores es 95 que es imposible agruparlos en tres conjuntos, por tanto nuestra solución es óptima y parece que vamos por buen camino.
Pero ¿qué ocurre en toda mudanza que se precie? Eso, que en el último momento aparece otro objeto, el recuerdo que te trajo tu suegra de Marina D’Or u otro número en nuestra versión 1-dimensional. Digamos que nos ha aparecido un 4. Me temo que vamos a necesitar una quinta caja para ese pobre 4 ya que no queda hueco en ninguna de las anteriores.
Sin embargo, si ponemos en el primer grupo al 12, el 8 y un 5, en el segundo 11, 10 y uno de los 4, en el tercero los dos 7 y dos 5, para el tercero nos quedarían tres 5, el 6 y un 4 para la cuarta caja y ¡caben!
Es que lo hemos hecho a lo loco, sin pensar… Podríamos haber ordenado antes los números, ¿no? Si lo intentáis con este mismo ejemplo, también os salen 5 cajas que, como acabamos de ver, no es un resultado óptimo.
Bueno, señores, vamos a usar el ordenador que hasta ahora lo tenemos muerto de risa en un rincón y se nos va a olvidar en la mudanza. Le pedimos que calcule todas las posibilidades. Tenemos 15 objetos, sabemos que no caben en tres grupos (suman más de 75, 3 cajas), por lo tanto tenemos que ver todas las formas de agruparlos de 4 en 4.
¿De cuántas formas podemos guardar 15 objetos diferentes en 4 cajas?
A ver, ¿cómo andamos de combinatoria? Sí, es a ti, no te escondas… Sin tener en cuenta, de momento, si suman más o menos de 25, lo que queremos saber es de cuántas formas se pueden asignar las etiquetas 1, 2, 3 y 4 (etiquetas de las cajas) a cada uno de los 15 elementos. Por ejemplo, como en la siguiente figura, el 12 va la caja 1, el 11 a la caja 4, el 7 a la caja 2…
Ése número, el número de formas posibles de guardar 15 objetos en 4 cajas, es CR 4 15, que no, no es ningún futbolista famoso, sino el número de combinaciones con repetición de 4 elementos, tomados de 15 en 15, es decir
Os dejo este enlace y este otro por si queréis recordar un poco de Combinatoria.
Nos de 816, pan comido para un ordenador. Sólo quedaría por ver, si en alguna de esas combinaciones, todas las cajas suman menos de 25. Claro que si no caben en cuatro cajas, necesitamos comprobar con 5: las posibles elecciones de 5 cajas son 3876, que tampoco es complicado. Y si no sirven 5, miraríamos si en 6 cajas, si no en 7…
Básicamente, puede que necesitáramos probar todos los posibles subconjuntos de los 15 elementos originales, este número es 2¹⁵ = 32.768 que es algo abordable. Pero el problema real es que el número de objetos que tenemos en una mudanza nunca es de 15, sino más bien 100 o 1000 o incluso más y en estos casos tendremos que comprobar 2¹⁰⁰ o 2¹⁰⁰⁰ y estos números ya son una miajilla más enormes.
¿Qué es lo que pasa aquí?
Lo que pasa es que el problema del empaquetamiento tanto en su versión 1-dimensional como k-dimensional para cualquier k es un problema conocido como de complejidad NP-dura. En román paladino esto viene a ser que no existe (ni tenemos esperanzas de que exista) ningún programa de ordenador que resuelva de forma óptima el problema del empaquetamiento en un tiempo razonable, entendiendo por razonable, en menos de varios milenios para una entrada de, digamos, 5.000 objetos.
Pero no hay que agobiarse, porque en Naukas tenemos a José Cuesta que ha hecho la mudanza de forma muy eficiente.
Pasad, os enseñamos el piso… Deseamos que os resulte confortable y vengáis muy a menudo.
¡Oiga, señor, disculpe! Esa esquina del sofá, sí, ésa, la que está suficientemente cerca del radiador para calentarse sin sudar, fresquita en verano cuando se abren las dos ventanas y con un ángulo saludable para ver la televisión, ésa está reservada… 😉
Soy profesora del área de Matemática Aplicada de la Universidad de Sevilla desde un maravilloso día soleado de Noviembre de 1995. Desde entonces he descubierto que la satisfacción de investigar es sólo comparable a la de contar y enseñar lo que has descubierto. Durante más de 10 años esto último se redujo al ámbito de mis clases en la Universidad y a las comunicaciones en congresos. Con la llegada de mis enanos se me planteó el reto de contarlo fuera del aula, en la alfombra del salón. Y oye, me gustó. Ahora dedico parte de mi tiempo libre a la divulgación, para niños de 9 a 99 años, consciente de que a todo el mundo le gustan las matemáticas, solo que algunos aún no lo saben. Mis coordenadas en: claragrima.com.