Un grupo muy conocido de juegos matemáticos lo constituyen aquellos en los que diversas personas o pertenencias deben cruzar un río en un bote en el que no caben todos simultáneamente. Un ejemplo es el del granjero que debe cruzar el río con un lobo, una cabra y una col. En el bote sólo caben el granjero y una de sus pertenencias, pero no puede dejar solos en una orilla a la cabra y al lobo, ni la col y la cabra, porque en cualquiera de estos casos el segundo se comería al primero. Una adaptación de este problema sale incluso en un capítulo de los Simpson.
[youtube]https://www.youtube.com/watch?v=li0RJRjAEBg[/youtube]
Los primeros juegos conocidos de este tipo se remontan al siglo IX y aparecen en el libro Propositiones ad Acuendos Iuvenes (Problemas para aguzar a los jóvenes) que se atribuye a Alcuino de York (732-804). En uno de ellos se planteaba el siguiente problema (traducido de [1]):
Propositio de tribus fratribus singulas habentibus sorores (versión en latín en [2]):
Tres hombres acompañados cada uno de ellos por su hermana han de cruzar un río. A cada hombre le atraen las hermanas de sus amigos. En el río encuentran un pequeño bote en el que sólo pueden subir dos personas al mismo tiempo. ¿Cómo pueden cruzar el río sin que ninguna mujer sea mancillada por un hombre?
Bien, quizás no es un ejemplo muy adecuado para la sociedad actual en la que aún existe discriminación hacia la mujer, aunque el problema se formuló hace doce siglos. Por suerte, el problema evolucionó con el tiempo y entre los siglos XIII y XV se hizo muy popular una versión en la que tres matrimonios pretendían cruzar el río, pero los maridos eran tremendamente celosos y no permitían que sus mujeres estuvieran solas con otros hombres… Ummhh, parece que tampoco solucionamos la situación. Más tarde se cambió por pares de amos y criados, pero esta formulación quizás es demasiado clasista.
A finales del siglo XIX apareció una variante del problema en la que en la orilla del río había tres misioneros y tres caníbales. Os voy a explicar el acertijo y cómo podemos utilizar matemáticas de forma muy sencilla para resolverlo. Pero dado que soy un fan de The Walking Dead me vais a permitir la licencia de cambiar a los caníbales por zombis.

Bien, formulemos el problema. Tenemos en un lado del río a tres misioneros y tres zombis que quieren pasar a la otra orilla con un bote en el que sólo caben dos personas. Para evitar que los zombis se coman a los misioneros, nunca puede haber más zombis que misioneros en ninguna de las orillas. Si estás pensando en que por qué no matar a los zombis y solucionar el problema con tres viajes, la respuesta es que los misioneros, por los votos prometidos, no pueden matar… a nadie. La pregunta ahora es: ¿cuál es el mínimo número de viajes necesario para que las seis… ejem… “personas” pasen a la otra orilla y en qué orden deben hacerlo?
A lo largo de la historia se han planteado muchas formas de solucionar este problema. Aquí vamos a plantear dos soluciones distintas: una más sencilla haciendo uso de la simetría del problema y otra escalable respecto al número de misioneros y zombis utilizando un grafo. ¿Tienes ganas de jugar y te cansaste de hacer sudokus? Coge papel y lápiz.
Uso de la simetría
En la primera solución empezaremos utilizando un procedimiento de fuerza bruta, pero aprovecharemos la simetría del problema para hacer la mitad del trabajo [3]. Representaremos con un dibujo la situación en cada momento de los misioneros, los zombis y la barca, de modo que las posiciones inicial y final de nuestro problema serían las siguientes:
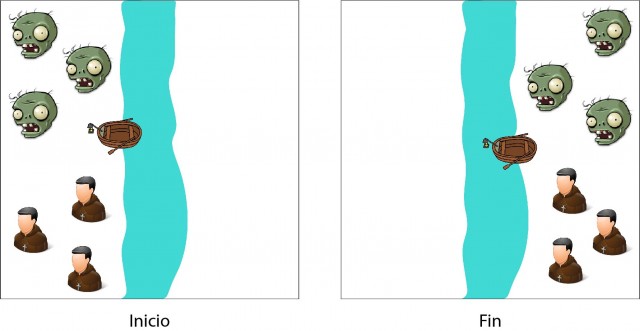
Fijémonos en la característica que nos ayudará a solucionar el problema: los estados de inicio y fin del problema son simétricos. Es decir, la solución al problema para pasar a los seis personajes a la otra orilla del río, aplicada en sentido inverso, nos permitiría devolverlos a la orilla inicial.
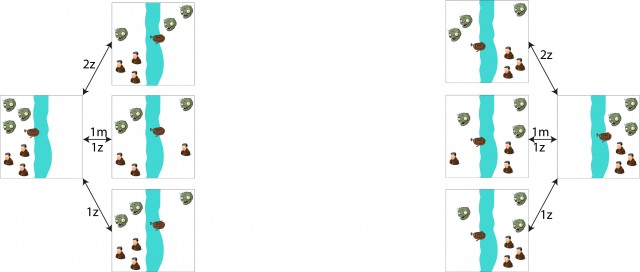
Vamos a empezar pensando en cuáles son los movimientos posibles a partir del estado de inicio. Recuerda que en ningún momento puede haber en alguna de las orillas más zombis que misioneros. En la siguiente figura tienes los únicos tres movimientos válidos, indicando en las flechas el número de zombis (z) y misioneros (m) que suben a la barca. Puedes pensar tú mismo por qué cualquier otro movimiento no resulta válido.
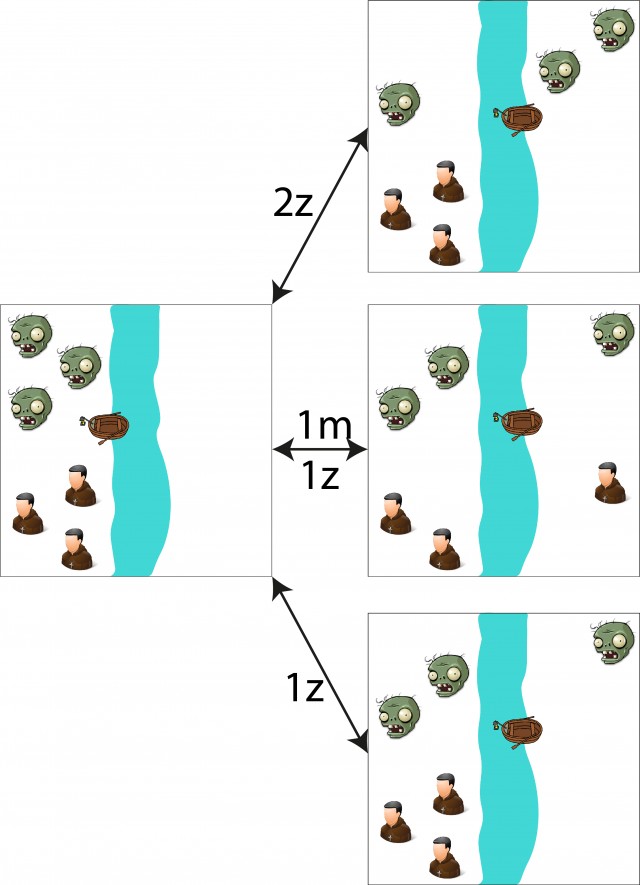
Aprovechando el principio de simetría, estas tres posibles soluciones (aplicadas en sentido inverso) nos servirían para volver de la orilla de llegada a la de partida. Esto nos permite dibujar la solución al problema desde el final.
No te despistes. Estamos intentando buscar la solución para llegar desde el estado de la izquierda al de la derecha. Construimos la solución desde la izquierda, pero utilizando la simetría del problema añadimos pasos a la solución por la derecha. ¿Te atreves a dar un par de pasos más? A continuación tienes la solución.
Y con sólo dar un par de pasos más, ya podemos conectar las soluciones desde la izquierda y la derecha y tener la solución al problema de forma gráfica (realmente, si te fijas bien, verás que hay cuatro soluciones posibles).

Como ves, el mínimo número de viajes en barca necesarios para pasar a la otra orilla es 11. Esta solución, aunque más sencilla de entender, presenta un problema: si variamos cualquiera de los parámetros iniciales la solución cambia e incluso se complica enormemente. Por ejemplo, ¿y si tenemos 4 misioneros y 4 zombis, y en la barca caben 3 personas? Además, tal y como se ha planteado, esta forma de solucionar el problema no es fácil de implementar con un programa de ordenador.
Uso de grafos
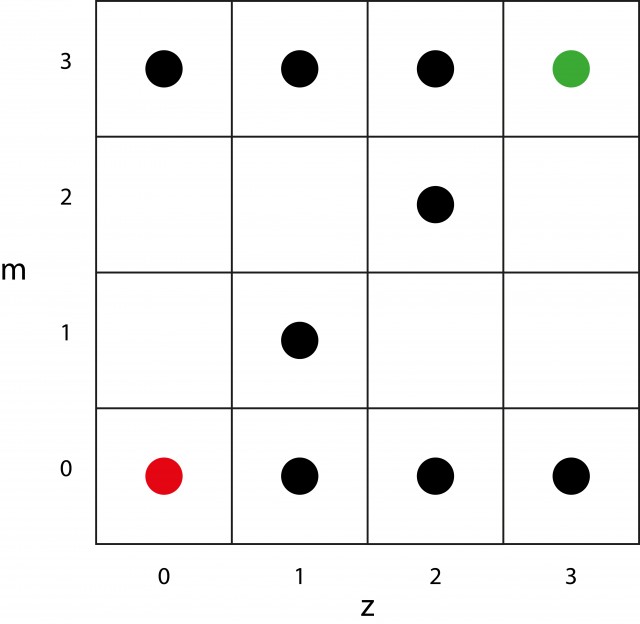
Para ver una solución que resuelva los problemas anteriores vamos a empezar definiendo numéricamente el estado de cada uno de los pasos de la solución. Si lo piensas un poco, para ello basta con apuntar cuantos zombis y misioneros hay en la orilla original, ya que el número y tipo de individuos en la otra orilla se obtiene mediante una simple resta. Así, si utilizamos la notación (z, m) para indicar los zombis y misioneros de la orilla izquierda, el problema puede plantearse como el paso del estado (3, 3) al estado (0, 0). Podemos representar estos estados utilizando una cuadrícula como la siguiente en la que el número m de misioneros se representa en el eje vertical y el número z de zombis en el horizontal [4]. Para que la entiendas mejor he añadido dos estados concretos y así puedas entender la relación con los ejes.
Obviamente no todos los estados de esta gráfica son posibles. Por ejemplo, el estado (2, 1) estaría prohibido porque habría más zombis que misioneros en la orilla inicial. De la misma forma, el estado (1, 2) tampoco sería posible porque habría el mismo problema, aunque en la otra orilla. En la siguiente figura se muestra con puntos los estados permitidos, indicando en verde el punto de inicio y en rojo el punto final.
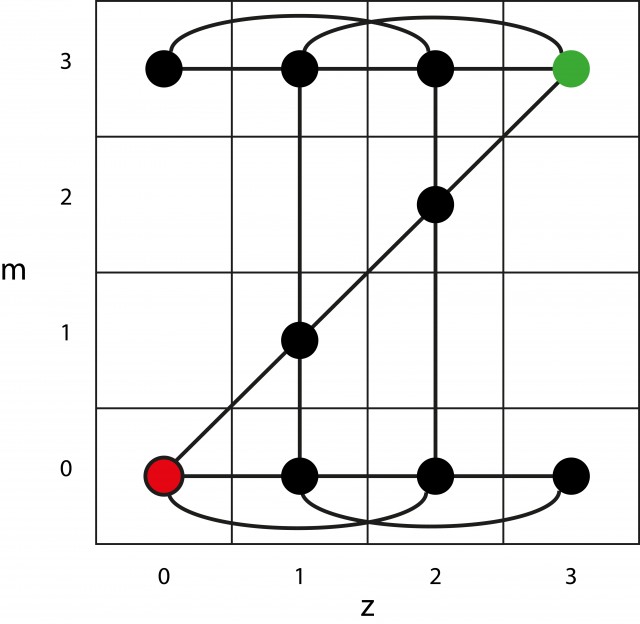
A esta gráfica le podríamos añadir líneas que conectaran los estados entre los que se puede transitar teniendo en cuenta que sólo pueden viajar dos sujetos en la barca. Te dejo como ejercicio que intentes añadir estas líneas al gráfico anterior, pero si no tienes ganas, se muestran en la siguiente figura.
Ahora sólo tenemos que encontrar el camino más corto entre el punto verde y el rojo siguiendo las líneas. La solución obvia es esta:
Es decir, sólo tres pas… ¡un momento! ¿No habíamos dicho que el número mínimo de pasos era 11?
No sé si te has dado cuenta, pero te he mentido intencionadamente al describir los estados. El problema es que en esta descripción de estados no se ha tenido en cuenta que cada punto representa realmente dos estados, según el bote esté en una u otra orilla. ¿Cómo podemos tener en cuenta este hecho para buscar una solución en el grafo del problema?
La clave para integrar la posición de la barca en el grafo es tener en cuenta que cuando la barca está en la orilla inicial, el estado que la describe perderá zombis o misioneros. Por ejemplo, si el estado actual del problema se describe por el estado (2, 2) y el bote está en la orilla inicial, el estado al que transite deberá tener menos de 4 individuos, porque el bote se llevará personas de dicha orilla. ¿Y cómo se traduce esto en nuestro grafo? Teniendo en cuenta que, en ese caso, sólo serán válidas aristas que vayan hacia la izquierda (menos zombis), hacia abajo (menos misioneros) o en diagonal hacia abajo e izquierda (restando un zombi y un misionero). Si, por el contrario, el bote está en la orilla final y regresa a la orilla de partida, el siguiente trayecto que se haga incrementará el número de individuos en la orilla original. Por lo tanto, en este caso los únicos movimientos permitidos serán hacia arriba, hacia la derecha, o ambos simultáneamente.
Por lo tanto, para buscar soluciones en el grafo desde el punto verde al rojo deberemos alternar aristas en un sentido y en otro, de forma que se representen los viajes de la barca en ambos sentidos. Si quieres pensar cómo hacerlo, coge papel y lápiz, y ¡adelante! A continuación te muestro una de las cuatro soluciones posibles. Fíjate en cómo se alternan los sentidos de las aristas de la solución.
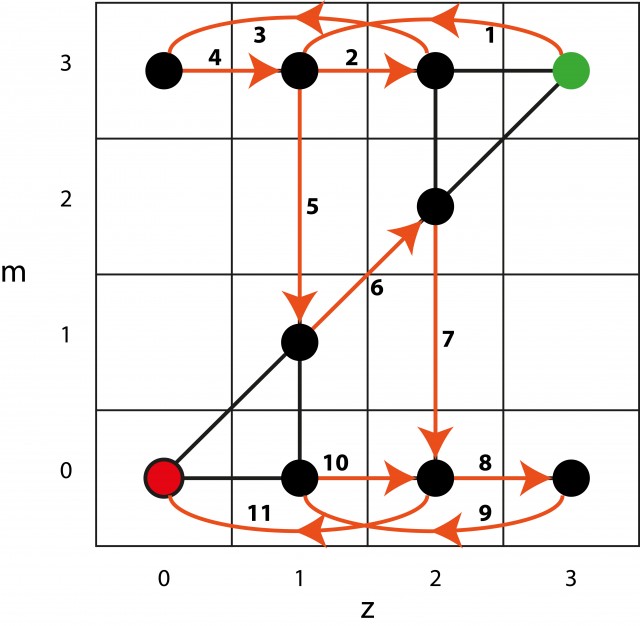
¿Cuál es la ventaja de esta solución respecto a la anterior? Para empezar, al estar representada cada solución como un par de números y utilizar un grafo es más sencillo resolver el problema mediante un programa informático. Pero además esta solución podemos aplicarla a cambios en los parámetros del problema. Por ejemplo, ¿cuál es el número mínimo de viajes si hay 4 zombis y 4 misioneros? ¿Y si dejamos que en la barca viajen tres individuos? Si (aún) tienes ganas de jugar y pensar más, te doy las soluciones a algunas de estas variantes.
- 4 misioneros, 4 zombis, bote con 2 individuos: no hay solución.
- 4 misioneros, 4 zombis, bote con 3 individuos: 9 viajes.
- 5 misioneros, 5 zombis, bote con 3 individuos: 11 viajes.
- 6 misioneros, 6 zombis, bote con 3 individuos: no hay solución.
Y volviendo al planteamiento del principio del texto sobre maridos celosos, ¿cómo afectaría a la solución que cada marido deba estar con su mujer en el lado correcto del río (a menos que la mujer esté sola)? En este caso, aunque parezca más complicado a simple vista, se puede demostrar que la solución es la misma que en el caso de los zombis: 11 pasos. Pero en cada movimiento hemos de pensar que en la barca no irá un hombre cualquiera, sino un marido en particular.
Si has tenido la paciencia de llegar hasta aquí y te has quedado con ganas de más zombis cruzando ríos, te propongo que trates de resolver este acertijo.
[youtube]https://www.youtube.com/watch?v=7yDmGnA8Hw0[/youtube]
Referencias y más información:
[1] Pressman, Ian; David Singmaster (June 1989). «»The Jealous Husbands» and «The Missionaries and Cannibals»». The Mathematical Gazette (The Mathematical Association) 73 (464): 73–81. doi:10.2307/3619658
[2] http://www.archimedes-lab.org/earlymathpuzzlers/alcuin_propositiones.html
[3] M. A. El-Dosuky1, M. Z. Rashad1, T. T. Hamza1, y A.H. EL-Bassiouny. Improving problem solving by exploiting the concept of symmetry. arxiv.org/pdf/1212.5776
[4] Martin Gardner, «Directed Graphs and Cannibals,» en The Last Recreations: Hydras,Eggs, and Other Mathematical Mystifications (PDF).
Soy doctor en ciencias químicas, e inicié mi investigación y doctorado en el campo de la química cuántica. Actualmente soy profesor titular de informática en la Universitat Jaume I de Castellón y colaboro como bioinformático con el grupo «Biología de retrotransposones» del centro de genómica y oncología GENYO de Granada. Mi investigación se centra en el estudio de los elementos genéticos móviles y microARN, así como su influencia en tumores y en enfermedades concretas como el síndrome de deleción 22q11.