Una de las diferencias que estamos aprendiendo a dejar atrás es la de la destreza, entendiendo ésta como la preferencia por usar la mano izquierda o la derecha (en realidad, no es una acepción aceptada aún por la RAE, pero no tengo otra forma mejor de traducir “handedness” así que permita el lector que la utilice en este contexto para indicar la tendencia a usar la mano izquierda o la derecha).
Atrás quedaron los tiempos en que a los niños zurdos se les obligaba a escribir con su mano menos hábil para convertirlos en “normales.” Persiste, sin embargo, una duda al respecto de zurdos y diestros: ¿cuál de ambos grupos es más listo?
Yo no me lo planteaba, pero he leído un artículo en el que se afirma que sí hay diferencia. Supuestamente, la preferencia por una u otra mano es una manifestación de la función cerebral. Se habla de la división del cerebro, del hemisferio izquierdo y derecho, de que un estudio de los años ochenta afirma que ser zurdo es un predictor de precocidad matemática… hay muchos modelos y son contradictorios, de modo que el tema está abierto.
Hace poco, El País se hizo eco de un estudio reciente sobre el tema, llevado a cabo por un grupo de investigadores de las universidades de Liverpool, Milán y Maastricht. Me llamó la atención el título que el diario creó para la noticia: “¿Tienen las personas zurdas más talento que las demás?” Me llamó la atención porque, según la conocida ley de titulares de Betteridge, si un titular está formulado como pregunta la respuesta suele ser “no, para nada”. A pesar de ello, el artículo sigue en el subtítulo: “este estudio indica que, en el caso de las matemáticas, puede que sea verdad”. Un titular interrogativo, un subtítulo dubitativo, pero a pesar de ello intrigante.
Me puse a leer el artículo del diario y no me dejó satisfecho, ya que la rotundidad del titular se diluye. Los autores no dicen realmente que sí, ni que no, sino que depende. Afirman que los zurdos aventajan a los diestros en resolución de problemas difíciles (“pauta particularmente clara en los adolescentes varones”, dicen) pero no hay diferencia cuando se trata de problemas sencillos. Tampoco es bueno ser diestro extremo, y terminan diciendo que “hay que ser prudentes a la hora de interpretar de qué mano prefiere servirse la gente, tanto si lo consideramos una señal de genialidad como un indicador de deficiencia cognitiva”, algo que no compromete pero queda bien.
No parece que se hayan mojado, así que fui a la fuente original y me bajé el paper (aquí), publicado en junio de este año en la revista Frontiers in Psychology. El título, sin ser interrogativo, sigue sonando tajante: “la relación entre destreza y matemáticas es no lineal y está moderada por género, edad y tipo de tarea.”
Lo primero que hay que tener en cuenta es que los resultados se basan en estudios sobre grupos muy concretos de población. Intervinieron más de 2.300 participantes, todos ellos escolares de colegios italianos, pero la mayoría son chavales entre 7 y 9 años (aunque uno de los experimentos se llevó a cabo con jóvenes de 14-17 años), y predominan los hijos de familias de clase media sin problemas de aprendizaje. Esto nos da el primer aviso: cualquier resultado que se obtenga será significativo en escolares italianos, no necesariamente en el resto de la población.
Dejaré de lado el detalle y me fijaré en un punto importante. Una de las cosas que más me llamó la atención es que los autores no consideran ser zurdo o diestro como dos opciones binarias sino como los extremos de un continuo. Es decir, se puede ser más o menos zurdo, hay grados. Para medirlo usaron el Inventario de Destreza de Edimburgo (EHI), que pregunta a los participantes sobre la mano que suelen usar para escribir, dibujar, lavarse los dientes y otros. A partir de ahí se define el índice H cuyos valores extremos oscilan entre -1 (zurdo total) y +1 (diestro total), de modo que H=0 indicaría un ambidextro. Me gusta la idea porque permite un estudio más continuo en lugar del “zurdo o diestro” habitual; y también permite aliviar el problema de infrarrepresentatividad de los zurdos, que son del orden del 10% de la población.
Se sometió a los voluntarios a un conjunto de pruebas escritas y se comparó el resultado de cada uno con su índice H. Cuando se pudo, se ajustaron los datos a una gráfica polinómica del tipo F(H)=a+bH+cH2+dH3+eH4, donde F(H) es el resultado del test correspondiente a un índice H determinado. He aquí las pruebas (llamadas “experimentos” por los autores, los resultados y mi comentario personal.
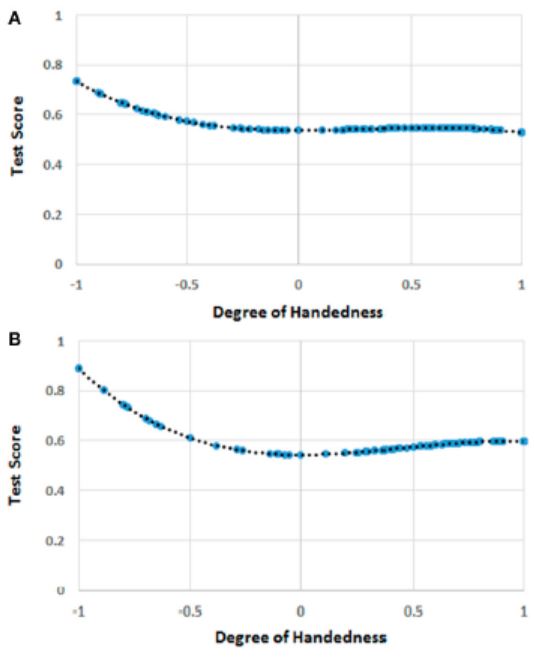
Aviso previo: por lo general paso de la corrección política chorra, pero eso podría causar confusión en este caso, así que usaré “chicos” para ellos, “chicas” para ellas y “todos” o “estudiantes” para el conjunto chicos+chicas. En cualquier caso, los datos obtenidos experimentalmente se indican mediante puntos azules, la curva en trazo discontinuo representa la tendencia.
Experimento 1 (relación entre destreza y precocidad matemática)
Muestra: 413 estudiantes (187 chicos, 226 chicas), edad 7-9. Prueba: 7 preguntas de test PISA.
Resultado: al hacer la gráfica vemos que tanto zurdos como diestros extremos sacan peor resultado que ambidextros (gráfica A). Sin embargo, la situación es diferente para las chicas (gráfica B), donde hay un repunte hacia la zona de destreza (“degree of handedness”) próxima a -0,5, lo que podríamos llamar “zurdas moderadas” Según los autores, esto descarta la hipótesis según la cual ser zurdo es un predictor de habilidad matemática (supongo que se refiere a zurdo extremo); y apoya la tesis de la desventaja de los extremos (ser radical no es bueno).
Comentario: El resultado para chicos no aparece porque, según los autores, no hay correlación, es decir, no se consigue una F(H) que ajuste bien los datos (para las chicas sí la hay). A pesar de ello me gustaría ver la gráfica para chicos, siquiera para ver qué pinta tiene. Vista la gráfica A y la B, cabría esperar que la gráfica para chicos fuese tipo “zurdo moderado” y con peores resultados. También querría saber por qué, si los chicos tienen entre 7 y 9 años, se les pasó un cuestionario de PISA para estudiantes de quince años. Quince años. No explican por qué lo hacen así, y me resulta extraño (aunque así se explica la baja puntuación o “test score”)
Experimento 2 (relación entre destreza y razonamiento matemático)
Muestra: 300 estudiantes (151 chicos, 149 chicas), edad 7-9. Prueba: 6 preguntas de test PISA (para estudiantes de 9 años)
Resultado: las gráficas para todos (A) y para chicos (B) muestra un comportamiento simétrico, con resultados máximos para los ambidextros y mínimos para zurdos/diestros radicales (H=±1). Ahora no hay correlación para chicas.
Cometario: como puede verse, cuando a los alumnos les ponen preguntas que pueden responder a su edad, los resultados mejoran (los “test score” son mejores). Los autores afirman que los extremos alcanzan la peor nota “pero sólo para chicos”, y afirman que el “género modera el efecto que la destreza ejerce sobre las notas en matemáticas”, pero carecemos de los datos de chicas para comprobarlo. Nuevamente me gustaría tener las gráficas de uno y otro género para contrastarlas.
Experimento 3 (relación entre destreza y habilidad aritmética)
Muestra: 160 estudiantes (78 chicos, 84 chicas), edad 5-7. Prueba: test de aritmética, tarea de rotación mental en 2-D
Resultado: ahora no se hace separación chico-chica. Los resultados globales indican una ventaja de los zurdos (H=-1) sobre los diestros (H=+1).
Comentario: me preocupa el pequeño número de zurdos (H entre -1 y 0) que puede haber desvirtuado los resultados, lo que significa que la “ventaja” de los zurdos puede ser espúrea. Los autores reconocen este mismo problema en su artículo, y sugieren que, en efecto, se trata de un resultado tipo “artefacto”.
Experimento 4 (relación entre destreza y habilidad aritmética)
Muestra: 798 estudiantes (417 chicos, 381 chicas), edad 5-7. Prueba: test de aritmética (operaciones básicas)
Resultado: ahora tenemos resultados por géneros (A: todos, B: chicos, C: chicas). En todos los casos, los radicales tienen menor puntuación, sean zurdos o diestros.
Comentario: me resulta llamativo el resultado por género. Si los chicos parecen ser mejores cuando están en el centro de la gráfica (ambidextros), las chicas puntúan mejor en la zona de zurdos/diestros moderados. En esto, no entiendo las conclusiones de los autores. Dicen que los estudiantes ambidextros (zona H=0) obtienen un resultado relativamente malo “especialmente las chicas” Los autores concluyen de ahí que eso apoya la idea de que los ambidextros tienen una desventaja en habilidades matemáticas “debido a su indecisión hemisférica”. Vale, lo entiendo en las chicas (gráfica C) ¡pero los chicos sacan la mejor nota justo en esa zona! ¿No hay indecisión hemisférica para ellos? Los autores parecen encogerse de hombros cuando se limitan a afirmar que dicha falta de indecisión “puede deberse a falta de potencia estadística” Lo siento, pero me suena muy raro.
Experimento 5 (relación entre destreza y habilidad aritmética en adolescentes)
Muestra: 641 estudiantes (211 chicos, 430 chicas), edad 14-17. Prueba: preguntas de test PISA y habilidades de rotación 3-D
Resultado: Tenemos los datos para todos (gráfica A) y para chicos (gráfica B). En ambos casos hay una fuerte tendencia hacia mejores notas para zurdos, y en este caso los “zurdos radicales” alcanzan las mejores calificaciones. Según los autores, esto refuerza la hipótesis de que los zurdos son más talentosos en matemáticas, pero solamente en chicos.
Comentario: una vez más, carecemos de datos sobre uno de los géneros. A la vista de las diferencias chico-chica vistas en el experimento 4 (el único que incluye datos separados para chicos y chicas), me pregunto hasta qué punto este olvido es accidental. Siguen escondiéndose datos que serían muy fáciles de graficar.
Veamos ahora, antes de seguir adelante, las conclusiones de los experimentos
Experimento 1: mejores resultados para chicas zurdas moderadas, peores para zurdos/diestros radicales
Experimento 2: mejores resultados para ambidextros, peores para zurdos/diestros radicales
Experimento 3: mejores resultados para zurdos, peores para diestros
Experimento 4: mejores resultados para chicas zurdas/diestras moderadas, peores para zurdos/diestros
Experimento 5: mejores resultados para zurdos, peores para diestros
No sé si seré el único, pero a mí me da la impresión de que esto no nos indica una tendencia clara.
Los autores parecen más preocupados en que haya “correlación”, esto es, que puedan representar la función F(H) como un polinomio, que en lo que ello signifique. Parece que, si hay correlación, hay algo detrás, y nosotros ya sabemos que correlación no implica causalidad. Los autores dicen que “la forma de la relación [esto es, de las gráficas] parece estar moderada por la edad, género y tipo de tarea hecha”. Y en efecto, está “moderada” en el sentido de que varía de un caso a otro, ¿pero cómo o según qué principios?
Los resultados aparentemente contradictorios de los experimentos me dejaron confuso, y me da la impresión de que los autores hacen encaje de bolillos para justificarlo:
– ¿Qué los resultados de Annett y Manning están en consonancia con los experimentos 1, 2 y 4 pero no con los otros? Bueno, será que la habilidad matemática en niños se basa en el nivel general de habilidades cognitivas y no en su habilidad espacial; y para justificarlo echamos mano a la teoría de los dos hemisferios (algo que me chirría pero en lo que no me meteré por falta de conocimientos).
– ¿Los experimentos 1, 2 y 4 tiran por tierra la hipótesis de Benbow sobre la ventaja de los zurdos? No hay que ser tan radical, que los experimentos 3 y 5 sí apoyan esa tesis. Es posible, dicen, que se debe a que los zurdos son un grupo heterogéneo “compuesto en parte de individuos dotados, en desarrollo e infradotados” (como si los diestros fuesen todos iguales) y puede que los zotes no aparecerán en los test debido a “auto-exclusión o selección académica” (hipótesis que rechazan a renglón seguido). Enseguida sugieren que quizá las diferencias entre zurdos y diestros es demasiado pequeña para que se vea en grupos pequeños (de menos de 5.000 estudiantes).
– ¿No se confirma la hipótesis de la indecisión hemisférica? También en esto jugamos con los experimentos: si algunos la desmienten, otros la confirman. Los autores parecen creer que, si tiramos una moneda al aire diez veces y algunas veces sale cara, la hipótesis “siempre que tiramos una moneda al aire cae de cara” se confirma. Lo siento, esto no funciona así. O cae de cara siempre o la hipótesis no vale.
– ¿Qué pasa con la variable género? A veces hay relación entre género y habilidad matemática, y a veces no. La justificación de los autores es que “la explicación no es simple.” Vale, lo acepto, pero entonces ¿para qué tanto intento de explicación? Para eso, prefiero un artículo que diga “aquí están los datos, y como ven hay muchas cosas raras, y no tenemos explicación así que usted mismo”. Me parecería más honrado y rápido.
El artículo acaba diciendo que las hipótesis en boga sobre la relación entre destreza y habilidad matemática “no son necesariamente irreconciliables” y con el habitual “hay que investigar más esto”.
A la vista de todo lo anterior, me da la impresión de que este artículo no resuelve nada, no aclara nada, y por supuesto no justifica titulares como “¿de verdad las personas zurdas tienen más probabilidades de ser geniales?” Si acaso, podríamos concluir que los escolares italianos de primaria puede que sean más hábiles en según qué cuestionarios de matemáticas, y eso con pinzas; pero eso de poder decir que los zurdos son más listos, o menos listos, que los diestros, ni mijita.
Disclaimer final: no ha sido hasta que me he puesto con el artículo que me di cuenta de que los principales autores del estudio son psicólogos, y la revista en que publicaron es de la rama de psicología. Lo digo porque sé que hay muchos psicólogos por ahí con piel fina, y cada vez que hablo del tema saltan irritados. Por lo que pueda valer, declaro no haber escogido este artículo para criticarlo porque sea de psicología. Con todo, ahora que sé que es un artículo de psicólogos, puedo decir que se nota. Lo siento, pero es lo que hay. Ya podéis llamarme de todo en 3, 2, 1…
(PD: Como ya habrás visto, astuto lector, este post es una violación flagrante de la ley de Betteridge. Soy así de destroyer)
Soy profesor titular de Física en la Universidad de Granada, padre y esposo, lector, escritor y divulgador científico por vocación. Encuéntrame aquí y en elprofedefisica.es. Recuerda: la ciencia mola, sólo que aún no lo sabes.