Clifford A. Pickover es todo un personaje en el mundo de la divulgación científica. Doctorado en 1982 en la universidad de Yale, por los departamentos de biofísica molecular y bioquímica, entró a trabajar en el centro de investigación Thomas J. Watson, de la empresa IBM, donde es editor de la revista IBM de investigación y desarrollo (IBM Journal of Research and Developement). Ha registrado nada menos que 502 patentes, que utilizan empresas como IBM, Google, LinkedIn, Ebay, Twitter, Yahoo! e incluso la marina de los EEUU. También ha escrito 50 libros, traducidos a muchos lenguajes, entre ellos el castellano, en los que trata temas relacionados con las matemáticas, la física, la biología, la creatividad, el arte, la informática, formas de representar gráficamente datos científicos, ciencia ficción y un largo etcétera. También escribe artículos sobre temas científicos y técnicos en varias revistas de prestigio, como Computers and Graphics, Odyssey magazine y Discover magazine.
Entre los muchos campos a los que ha dedicado su atención Pickover, destaca el estudio de los objetos fractales, que pertenece al ámbito de las matemáticas, pero que tienen aplicaciones en otros campos, como la física y la biología, para modelar sistemas con dinámica compleja o caótica, o construir modelos de crecimiento de organismos vivos, por poner solo unos pocos ejemplos. Los objetos fractales son bastante populares, ya que, al representarlos, podemos obtener unos gráficos sorprendentes y con una enorme variedad de formas y colores. De hecho, se utilizan mucho en infografía para obtener texturas y formas realistas de diversos materiales y organismos, como las plantas, por ejemplo. En el presente artículo voy a hablar de unos objetos fractales en concreto, descubiertos por Pickover, muchos de los cuales presentan formas que recuerdan a microorganismos o extraños seres procedentes de otro mundo, de ahí el nombre de biomorfos.
Para entender el proceso que lleva a generar estos curiosos seres virtuales, empecemos por la idea de partida de la que proceden: el conjunto de Julia, llamado así en honor del matemático francés Gastón Julia, quien lo estudió a principios del siglo XX. El procedimiento para construir este conjunto es bastante sencillo. Partimos de una función de variable compleja, que puede ser tan sencilla como esta:
F(z) = z2 + c
Donde z es una variable que toma valores en el dominio de los números complejos, y c es una constante, que también es un número complejo. Con esta función construimos un sistema dinámico, por el procedimiento de darle un valor a z, calcular F(z), y usar este resultado para volver a calcular el valor de la función, repitiendo el proceso una y otra vez. De esta manera, la salida del sistema se vuelve a introducir como entrada en el paso siguiente, y podemos observar cómo evoluciona el sistema a lo largo del tiempo. A la serie de números que vamos obteniendo se la conoce como órbita del valor z inicial en el sistema; para cada valor de z pueden suceder dos cosas: o bien la órbita es estable, y los valores se mantienen siempre dentro de una zona acotada del plano complejo, o bien es inestable, lo que significa que los valores se alejan (escapan) hacia el infinito. Es algo parecido a colocar un satélite en órbita alrededor de la tierra y calcular en qué posiciones lo podemos situar para que permanezca en órbita y en cuales se perderá en el espacio exterior. Pues bien, el conjunto de Julia de una función es el conjunto de todos los puntos que tienen órbitas estables para la función dada.
El caso es que, al representar gráficamente el conjunto, obtenemos multitud de formas sorprendentes, que varían con la función utilizada y con el valor de la constante c. Este es el conjunto de Julia para F(z)=z2+c, con c = 0.36 + 0.1i:
A la izquierda se encuentra representado, en color negro, el conjunto completo; a la derecha podemos ver un detalle ampliado de una pequeña zona. No importa cuánto ampliemos cualquier zona de la frontera del conjunto, pues siempre presenta un aspecto igual de enrevesado. Su contorno tiene una longitud infinita.
Al hacer los cálculos en un ordenador, evidentemente no podemos realizar infinitas iteraciones para averiguar si un punto pertenece o no al conjunto; pero existe una propiedad muy útil que facilita enormemente el procedimiento: si uno de los valores de la serie tiene un módulo mayor que 2, es seguro que la serie escapará hacia el infinito, y podemos descartar el punto. De este modo, solo es necesario realizar unas pocas iteraciones para decidir si un punto pertenece o no al conjunto. Esta propiedad también se utiliza para colorear los gráficos y hacerlos más vistosos; los puntos del conjunto se dibujan con un color y, para el resto, se utiliza un color diferente en función del número de iteraciones que hayamos necesitado para decidir que el punto no pertenece al conjunto.
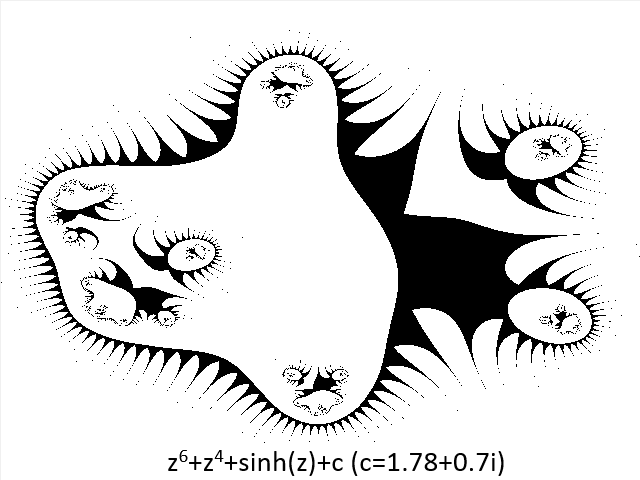
Pero volvamos a Pickover y a sus biomorfos. Pickover añadió a este algoritmo para calcular conjuntos de Julia una condición adicional: además de comprobar si la órbita del punto escapaba al infinito, ni la parte real ni la imaginaria de los números complejos de la serie podían ser mayores que un determinado valor parametrizable. El caso es que confundió la operación lógica AND con la operación OR al implementar esta condición en el algoritmo, lo que tuvo como consecuencia que se incluyesen en el conjunto muchos más puntos, dando lugar a representaciones gráficas como la siguiente:
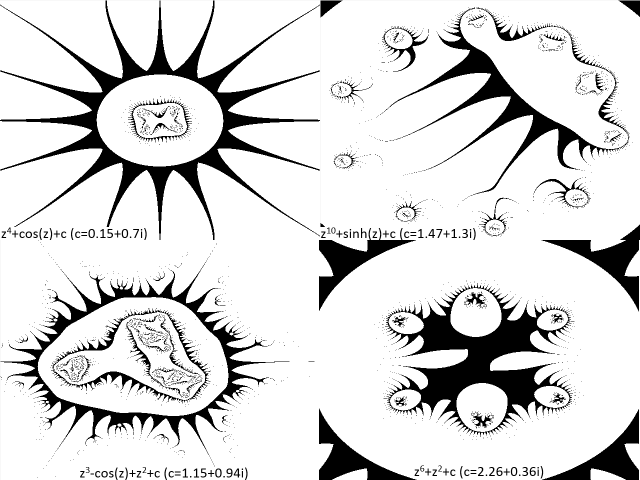
Aquí os dejo otra serie de capturas con más y más biomorfos. En los enlaces que acompañan al artículo os dejo uno al sitio CodeProject, dónde podéis descargar el programa, junto con el código fuente, con el que he generado estos dibujos, desarrollado por mí. Las explicaciones están en inglés, pero es un programa muy sencillito que funciona solo. También os dejo un enlace a la página personal de Pickover, en la que aparecen todas sus patentes y libros, además de más información sobre el autor.
Este artículo nos lo envía Miguel Díaz Kusztrich, desarrollador en varios lenguajes desde los años 80 del pasado siglo, habiendo trabajado en múltiples áreas, desde los videojuegos, pasando por la electromedicina, multimedia, inteligencia artificial o el e-learning hasta la logística industrial, a la que me dedico actualmente. También soy un gran aficionado a las ciencias en general, y en especial a las aplicaciones de la informática y la tecnología a las mismas. Tengo dos blogs, desarrollados por mí, uno dedicado a la programación (http://software-tecnico-libre.es) y otro más personal, dedicado a una gran variedad de temas (http://filosofia-y-lo-que-surja.net), algunos de ellos también relacionados con la ciencia.
Referencias y más información:
Geometría fractal, algorítmica y representación. De Javier Barrallo Calonge, editorial Anaya.
Clifford A. Pickover homepage: http://www.pickover.com/
CodeProject: The astounding Pickover biomorphs, por Miguel Diaz Kusztrich:
https://www.codeproject.com/Articles/1217543/The-astounding-Pickovers-biomorphs
Si tienes un artículo interesante y quieres que lo publiquemos en Naukas como colaborador invitado, puedes ponerte en contacto con nosotros.