
La epidemiología es una de esas ciencias de frontera. Se encuentra en el difuso límite entre las matemáticas y la medicina. Se alimenta de conocimiento de ambas para proponer modelos, conclusiones y políticas. Pero el caracter fronterizo se manifiesta también en su práctica en tiempos difíciles. Las epidemias son crisis muy duras que afectan directamente a multitud de personas, arrebatando antes de tiempo a seres queridos. Sentimos también, indirectamente, el impacto sobre nuestras sociedades y economías.
Muchos, en busca de un marco ideológico para entender las penalidades por las que estamos pasando, asimilan la epidemia a una guerra. Con enemigos, aunque invisibles, que buscan nuestra destrucción. Los epidemiólogos se mueven en terreno inestable, donde las suposiciones de un día pueden variar al siguiente. Nada de esto impide someterlos a la tensión de la búsqueda de certidumbres de una población que sufre. Así vivimos estos días aciagos, en plena crisis del coronavirus.
Modelos epidemiológicos de juguete
Una de las herramientas más importantes en la conceptualización de la transmisión de la enfermedad es el modelo epidemiológico. Luchando por entender lo que está pasando hay quien ha desenvainado la función exponencial, un concepto matemático básico para entender muchos aspectos de la realidad que nos rodea, si fuéramos a la vez conscientes de sus graves limitaciones.
Modelar una realidad con una función exponencial supone, como poco, obviar el hecho de que la capacidad infecciosa del virus no puede ser perfecta y que la población susceptible de infectarse no es infinita ni continua. Es un ejemplo quintaesencial de «vaca esférica», muy querido por ingenieros, físicos y economistas en busca de certidumbre. También es dramáticamente incompleto. Querer entender algunos aspectos de la epidemia con una exponencial es legítimo. Pretender extraer recomendaciones prácticas de política sanitaria —tácticas y estrategias, si nos plegamos a la retórica bélica— a partir de una exponencial desnuda es, en el mejor de los casos, irresponsable.
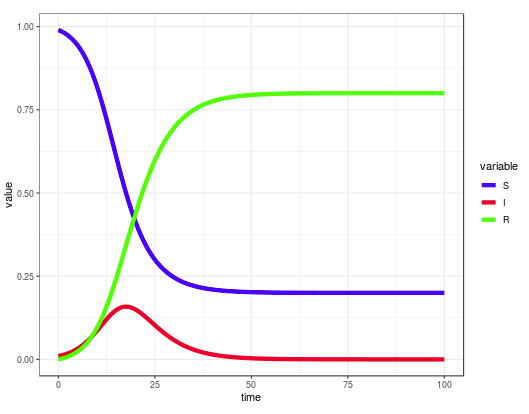
En el siguiente escalón de los modelos pueden encontrarse los modelos compartimentalizados simples. La población, bajo un conjunto de supuestos restrictivos, se clasifica en tres estados posibles: susceptibles, infecciosos y recuperados. Se establecen las posibles transiciones entre ellos y se deriva la evolución de la enfermedad en la población a partir de un conjunto de ecuaciones diferenciales. De aquí sale el concepto de número de reproducción básico o R₀: el número de casos esperable, en promedio, a partir de un primer infectado en una población completamente sana. Es sencillo de asimilar: si R₀ es menor que uno, el patógeno tenderá a la extinción. Si, por el contrario, R₀ es mayor que uno, nos encontraremos con una potencial crisis epidémica. Valores mayores de R₀ sugieren infecciones más virulentas.
La pandemia de COVID-19 tiene un R₀ estimado entre 1,4 y 4,2, según fuentes. ¿Significa eso que podemos estar tranquilos? En absoluto: la famosa gripe de 1918 presentó un R₀ entre 1,4 y 2,8. El impacto de una epidemia no se reduce a un parámetro sacado de un modelo cuyas simplificaciones radicales lo alejan de la realidad.
Avanzando en la conceptualización de las epidemias
A partir del modelo SIR, los epidemiólogos han trabajado para afinar sus herramientas incorporando en los modelos más aspectos de la realidad, tal y como se van conociendo. Aspectos demográficos como los nacimientos y, sobre todo, las muertes, permiten discriminar en ese cajón de sastre de los «recuperados» del modelo SIR introduciendo distinciones socialmente relevantes. No es lo mismo estar curado e inmunizado que fallecido en una morgue. Nuevos estados introducen diferentes detalles: una categoría de expuestos permite tener en cuenta a aquellos individuos infectados que no tienen, aún, capacidad de transmitir la enfermedad (modelo SEIR). Si existe inmunidad previa, heredada o maternal en parte de la población, puede tenerse también en cuenta (modelo MSIR). Si la inmunidad obtenida en la recuperación es temporal —como en el caso de la gripe estacional— los recuperados pueden volver a engrosar las filas de los susceptibles (modelo SIRS).
Todos estos modelos pueden combinarse entre sí como las herramientas de una caja, como hicieron previamente Pablo Rodríguez y Francis Villatoro previamente aquí, en Naukas [1][2]. Las limitaciones a las que se enfrentan los epidemiólogos tienen una naturaleza doble: por un lado, las transiciones entre compartimentos deben ser calibradas de acuerdo a parámetros observados en la población durante una epidemia. Por el otro, el aumento de complejidad de los modelos hace más complejo su tratamiento, y obtener recomendaciones de política sanitaria a partir de ellos se convierte en un peligroso juego de gato y ratón, solo que con multiples gatos, legiones de ratones no exactamente iguales, mediciones inexactas sujetas a criterios no óptimos y posiblemente cambiantes y personas muriendo ante la impotencia de una ciudadanía que exige directrices y respuestas claras.
El modelo del grupo MOMAT
El grupo de investigación MOMAT del Instituto de Matemática Interdisciplinar de la Universidad Complutense de Madrid está trabajando contrarreloj en plena crisis, en constante contacto con las autoridades sanitarias del país. Benjamín Ivorra, Míriam Ruiz Ferrández, María Vela y Ángel Manuel Ramos han publicado en una preimpresión un nuevo modelo epidemiológico de tipo θ-SEIHRD. Los estados que tiene en cuenta son:
- Susceptibles (S): personas no infectadas.
- Expuestas (E): personas que incuban la enfermedad, no muestran síntomas y, además, podrían transmitirla.
- Infectados detectados (Id): persona que muestra síntomas y entra en el sistema de detección de las autoridades sanitarias.
- Infectados no detectados (Iu): persona que muestra síntomas pero no es detectada por el sistema por cualquier motivo.
- Hospitalizados o en cuarentena domiciliaria (HR): contabilizado por las autoridades, todavía puede infectar a otros.
- Hospitalizados que morirán (HD): también capaces de seguir infectando.
- Fallecidos (D).
- Recuperados (Rd): recuperados en el hospital. Han desarrollado inmunidad y, al menos temporalmente, no seguirán propagando la enfermedad.
- Recuperados (Ru): recuperados en las mismas condiciones que Rd, pero no detectados.
![Diagrama resumen del modelo propuesto por el equipo de MOMAT para describir la propagación de la pandemia de COVID-19. Fuente: [1].](https://naukas.com/fx/uploads/2020/04/modelo_MOMAT_v2.png)
- Aislamiento: aplica a enfermos declarados bajo control por personal sanitario.
- Cuarentena: restricción de movimientos controlada por las autoridades (fuerzas y cuerpos de seguridad estatal).
- Seguimiento: obtención de mapas de contacto de infectados para determinar posibles afectados adicionales, no detectados previamente.
- Incremento de los recursos del sistema de salud: camas disponibles, personal sanitario, respiradores y otros elementos tecnológicos.
- Incremento del número de pruebas de detección realizadas.
Un aspecto novedoso de este modelo es la introducción de un método de estimación de la fracción θ (casos detectados frente a casos totales), lo que permite estudiar directamente el impacto de los casos que no entran en el sistema, incluidos asintomáticos, sobre la propagación de la enfermedad.
Resultados preliminares
Según el modelo del grupo MOMAT, el número de reproducción básico (R₀) de COVID-19 es de 4,2250, uno de los más altos estimados en la literatura. Más importante: el porcentaje de casos no detectados, incluidos asintomáticos, sería del 51%, habiendo causado estos alrededor del 37% de las infecciones. Las medidas de control adoptadas han sido esencialmente eficaces en China, aunque se puede observar un retraso de dos semanas entre su aplicación y sus primeros efectos.
Limitaciones y acciones futuras
La calibración de este modelo se ha realizado mediante datos recogidos durante el desarrollo de la epidemia en China. Estos datos tienen limitaciones e inexactitudes que obligan a la aplicación de algoritmos adicionales. Se comparan las salidas conocidas de las diferentes compartimentos del modelo en varias fechas para especificar un problema de optimización multiobjetivo de sus parámetros, usando para ello un algoritmo genético [4].
El trabajo del equipo del MOMAT está actualmente en revisión para afinar las características del modelo respecto de los datos medidos en la epidemia en España. Sin embargo, su trabajo permite ya avanzar varias conclusiones preliminares:
- El porcentaje de infectados no detectados (Iu) es muy elevado y está dominando la evolución de la pandemia. Es por tanto imperativo aumentar el número de tests realizados, por cualquier medio a nuestro alcance.
- La tasa de infectados detectados que, a su vez, son personal sanitario es muy elevada y podría limitar la eficacia de cualquier respuesta futura a corto plazo ante la pandemia. Es necesario mejorar sus medidas de protección con caracter inmediato.
- Las medidas de cuarentena están mostrando una eficacia limitada en la contención de la enfermedad, por lo que se recomienda hacerlas más restrictivas.
Agradecimientos
Agradezco encarecidamente a María Vela su ayuda para la realización de este artículo. Todos los errores que contenga son de mi cosecha.
Para saber más
[1] Rodríguez, P. (18/03/2020). Un matemático en cuarentena. Naukas. Visitado el 29/03/2020, en https://fuga.naukas.com/2020/03/18/un-matematico-en-cuarentena/.
[2] Villatoro, F. R. (14/03/2020). El modelo SEIRV aplicado a la epidemia de coronavirus en Wuhan, China. Naukas. Visitado el 29/03/2020, en https://francis.naukas.com/2020/03/14/el-modelo-seirv-aplicado-a-la-epidemia-de-coronavirus-en-wuhan-china/.
[3] Ivorra, B., Ruiz-Ferrández, M., Vela-Pérez, M., y Ramos, A. M., (01/04/2019). Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. The case of China. Preimpresión. doi: 10.13140/RG.2.2.21543.29604. Consultado en https://www.researchgate.net/publication/340114074_Mathematical_modeling_of_the_spread_of_the_coronavirus_disease_2019_COVID-19_considering_its_particular_characteristics_The_case_of_China.
[4] Un algoritmo genético es una búsqueda heurística de un conjunto de parámetros para establecer los valores extremos (mínimos o máximos) de una serie de funciones objetivo. Partiendo de una primera generación, se introduce un amplio conjunto de mutaciones (variaciones controladas) en los parámetros, se reevalúan las funciones objetivo y se selecciona la generación más «exitosa». Este proceso se repite hasta que se cumple algún criterio de estabilidad entre resultados de diferentes generaciones.
Otra instancia más de Homo sapiens. De pequeño quiso ser científico, astronauta y ganar dos premios Nobel. Conforme fue creciendo estas aspiraciones sufrieron progresivos recortes: finalmente se quedó en ingeniero de telecomunicaciones. Con más años de experiencia de los que quiere reconocer en la intersección del tren con las tecnologías de la información, trabaja en la actualidad en el apasionante campo de la innovación ferroviaria como director de innovación en Telice, S.A.. Tímido en rehabilitación y con más aficiones de las que puede contar, cuando tiene tiempo escribe sobre cualquier cosa que le llame la atención: ciencia, espacio, ingeniería, política…
