
Cuando nos aproximamos a un problema matemático, muchas veces tenemos problemas para conceptualizarlo, o traducirlo, directamente a una ecuación.
Si tenemos un problema que dice que “la edad de Ana es dos veces la edad de Juan, más 3 años”, es un problema muy sencillo de poner en una ecuación. Si decimos que la edad de Ana es X y la edad de Juan es Y, entonces:
X = 2Y + 3
El problema es sencillo porque es una relación fija entre dos cantidades.
Pero en el caso de problemas en el que existen cambios de cantidades en el tiempo, mucha gente tiene dificultad para conceptualizarlos de forma inmediata, de modo que podemos recurrir a la “tanteometría”. O sea a empezar a sustituir algunos valores, o a crear tablas de relaciones, para poder visualizar y “tantear” cómo debe ser la solución.
Una palabra más correcta sería “proceso heurístico”, que quiere decir, un método que no necesariamente es óptimo, pero que de todas formas nos lleva a entender cómo llegar a la solución.
Veamos un problema clásico: dos velas que se van consumiendo.
LAS DOS VELAS
Tenemos dos velas de la misma altura, pero cuya concentración de cera es ligeramente diferente, lo que causa que una se consuma más rápido que la otra.
La vela A se consume por completo en 8 horas, mientras que la vela B tarda 10 horas en consumirse.
La pregunta es: ¿cuánto tiempo debe pasar para que la vela A tenga la mitad de la altura de la vela B?
TANTEANDO
Para alguien con práctica, es sencillo hacer la traducción a una ecuación de forma inmediata, pero para alguien con menos experiencia puede resultar confuso. La relación entre las velas es muy fácil de entender, así como lo que se pregunta, pero aún así mucha gente encuentra difícil traducirlo a una ecuación.
Así que, para poder entender lo que debemos hacer… ¡es tantear!
Para eso, hagamos una tabla de cómo se van consumiendo las velas en el tiempo. ¿Cómo lo hacemos? Pues primero que nada vamos a poner eso de “tarda X horas en consumirse” en otros términos:
– La vela A consume 1/8 de su altura cada hora.
– La vela B consume 1/10 de su altura cada hora.
Perfecto. Como segundo paso, vamos a asumir una altura para ambas velas, que pueda dividirse entre 8 y entre 10. Así que 8×10 = digamos que ambas velas miden 80 cm.
– La vela A consume 80/8 = 10 cm cada hora, y
– La vela B consume 80/10 = 8 cm cada hora.
Veamos cómo se van consumiendo:
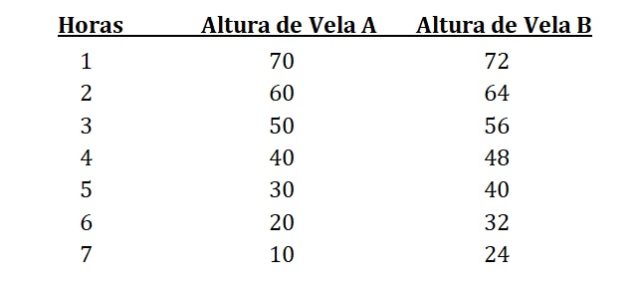
¡OK, ya lo podemos ver con claridad! El problema es que nuestra solución no es una cantidad exacta de horas, sino que va a ser un momento entre la hora 6 y la 7, cuando la vela A sea la mitad exacta de B.
LAS ECUACIONES
Pero al ver así las cantidades, ya podemos hacer ecuaciones:
La ecuación que describe el comportamiento de la vela A en relación al tiempo, es así:
A = 80 – 10t
O sea, la altura de A en cualquier momento, es 80 (la altura original) menos 10t: o sea la velocidad de 10 cm/hr, multiplicada por el tiempo transcurrido. Podemos revisarlo:
La altura en la hora 2 es:
80 – (10 x 2) = 80 – 20 = 60
Revisamos la tabla… ¡correcto! Y lo bueno es que esta ecuación funciona para cualquier cantidad de tiempo: por ejemplo si queremos saber la altura después de 3 horas y media:
A = 80 – (10 x 3.5) = 80 – 35 = 45
Con esta misma lógica, construimos la ecuación para el comportamiento de B, y tenemos las dos ecuaciones listas:
A = 80 – 10t
B = 80 – 8t
¡Listos!
Ahora, lo que queremos es encontrar un tiempo t muy especial, en el que la altura de A es la mitad de la altura de B. Esto es, el momento en que A = B/2.
Y como sabemos exactamente cuánto es A y B en cualquier momento, gracias a nuestras dos ecuaciones, sustituimos y ponemos así:
(80 – 10t) = (80 – 8t)/2
Esta ecuación se resuelve de forma muy sencilla:
80 – 10t = 40 – 4t
40 = 6t
t = 40/6t = 6 2/3
El momento exacto en el que A tiene la mitad de la altura de B, es 6 horas y 40 minutos después de haber sido encendidas ambas.
¡Tanteometría que nos lleva a la ecuación correcta!
Nací en México y vivo en China desde el 2000, donde estudié idioma e historia, y luego fui investigador visitante en el Centro Internacional Wan Lin Jiang de Economía y Finanzas, así como profesor de economía e historia para extranjeros en la Universidad de Zhejiang. Actualmente dirijo el Mexico-China Center y doy conferencias acerca de ciencia y cooperación tecnológica internacional.
