[youtube]http://www.youtube.com/watch?v=lf933URMdEY[/youtube]
Los caminos de la curiosidad son impredecibles. Afortunadamente. Durante la pasada edición del evento Amazings 2011, un colaborador de este mismo blog, César Tomé, me preguntó sobre el puente Zubizuri que usábamos a diario para cruzar la ría:
«¿Es un parábola o una catenaria?»

«No lo sé, supongo que una catenaria», contesté yo. «La catenaria es muy ‘apañá’ para temas arquitectónicos».
Más tarde, al volver a cruzar el puente, me asaltó la curiosidad y recurrí a Google para confirmar o desmentir esta teoría. Es una parábola.
Pero no quedó ahí la cosa porque, como nos pasa a todos cuando navegamos en busca de información, empecé a bucear en temas de arquitectura y buceando, buceando llegué, no śe cómo porque no lo recuerdo, a una estudios sobre tensegridad y su uso en la arquitectura, por ejemplo en el diseño de la Montreal Biosphère.
O en el del Kurilpa Bridge en Brisbane.
«Tensegridad…el caso es que me suena ese término»
Sigo navegando arrastrada por las corrientes tenségricas, y arribo a páginas de arte, y pienso: «Pero si hay una estructura de este tipo en la puerta de la ETSII, la veo todas las mañanas»
Y sigo buscando, y encuentro artículos de biología y citoesqueletos… Maravilloso. Encuentro trabajos de Donald Ingber que atribuyen a la estructura de las células, al citoesqueleto, principios inherentes de la tensegridad,
o sobre biotensegridad, estudiando la geometría de nuestro esqueleto
Pero en medio de este fluir por aguas científicas me encuentro, ¿cómo no?, el chapapote: una magufada, otra más, de Carlos Castaneda que interpreta o utiliza la tensegridad como el ritual mágico que nos ayuda, sin ningún lugar a dudas, a alcanzar la más suprema, supremísima de las felicidades. Por lo visto, para ello sólo hay que realizar algunos movimientos, aprendidos de los chamanes nativoa americanos en Mexico.
[youtube]http://www.youtube.com/watch?v=lauKs7tbtV8[/youtube]
Pero es que si sigues buceando, hasta cremas milagrosas encontrarás que usan el concepto de tensegridad para conseguir la eterna juventud, claro.
Madre mía…
También se ha usado el concepto, tiene más sentido, para el diseño de bicicletas,
de sillas
«Ya sé de qué me suena lo de tensegridad, algo he oído en Teoría de Grafos»
Efectivamente. La comunicación que abre el congreso Convexity, Topology, Combinatorics and beyond y al que tenía previsto asistir unos días más tarde será impartida por Robert Connelly, que no sé si será familia del creador de Harry Bosch, pero sí es una de las voces más importantes en Tensegridad en la comunidad matemática.
Y también @imatematicas, en su infatigable labor de divulgación con sus estudiantes, me había hablado de que las habían hecho en su instituto.
«Pues nada. Matemáticas, arquitectura, biología, magufada,…esto va para Amazings.es…»
Vamos entonces a formalizar todo esto un poco que nos entendamos.
Si miramos en la wikipedia, por ejemplo, la definición de tensegridad tenemos que
O sea, que son estructuras donde algunos elementos están tirantes, tensos y otros están apretados, comprimidos; pero en equilibrio: aquí o nos movemos todos o no se mueve nadie.
El matemático español Miguel de Guzmán dio su propia definición, más matemática
Según ésta última definición, si en un segmento asignamos las direcciones de los vectores así
 éste será un elemento tensado, mientras que si la asignamos como nos muestra la siguiente figura será un elemento comprimido.
éste será un elemento tensado, mientras que si la asignamos como nos muestra la siguiente figura será un elemento comprimido.
 Tal y como nos explican R. Connelly y A. Back en Mathematics and Tensegrity, si dejamos a un lado los detalles físicos de la construcción, una tensegridad no es más que una configuración de puntos que satisfacen unas ciertas restricciones simples sobre distancias.
Tal y como nos explican R. Connelly y A. Back en Mathematics and Tensegrity, si dejamos a un lado los detalles físicos de la construcción, una tensegridad no es más que una configuración de puntos que satisfacen unas ciertas restricciones simples sobre distancias.
Muchas de las estructuras de tensegridad están construidas con dos tipos de elementos: cables y tirantes (o puntales). Los cables mantienen los puntos cercanos y los tirantes los mantienen alejados. Los puntos conectados mediante un cable se pueden acercar todo lo que queramos pero no se pueden alejar más allá de la longitud del mismo, es decir, los cables se pueden comprimir pero no estirar. Por otro lado, los puntos conectados en la estructura mediante tirantes se pueden alejar tanto como se desee pero no se pueden acercar más que la longitud del tirante, o lo que es lo mismo, los tirantes se pueden estirar pero no encoger. En la mayoría de las estructuras tenségricas los tirantes son sustituidos por barras rígidas, que no estiran, como por ejemplo, las que tenemos en la entrada de la ETSII. Pero estas barras podrían sustituirse por tirantes sin sacrificio de la estabilidad. Entendiendo por estabilidad de la estructura, que cualquier movimiento continuo de cualquiera de los elementos, sigue respetando las restricciones sobre distancias entre las parejas de puntos conectadas por cables, tirantes o barras.; como decíamos hace unas líneas, o nos movemos todos o no se mueve nadie.
Si nos fijamos en la siguiente figura, conocida como la X de Snelson, donde los tirantes se han representado con línea continua y los cables con discontinuas, es fácil intuir que no es posible ninguna modificación de la estructura. Es rígida.
 Sin embargo, si intercambiamos los papeles de cables y tirantes, obtenemos la siguiente estructura
Sin embargo, si intercambiamos los papeles de cables y tirantes, obtenemos la siguiente estructura
 que no es rígida como podemos ver en la siguiente figura, es posible plegar los tirantes, acortando los cables y por lo tanto, modificando las distancias iniciales entre parejas de puntos.
que no es rígida como podemos ver en la siguiente figura, es posible plegar los tirantes, acortando los cables y por lo tanto, modificando las distancias iniciales entre parejas de puntos.
 Ahí está la belleza de las construcción de tensegridades, en conseguir una configuración aparentemente frágil pero absolutamente estable o rígida.
Ahí está la belleza de las construcción de tensegridades, en conseguir una configuración aparentemente frágil pero absolutamente estable o rígida.
El nacimiento de la tensegridad tiene, como cualquier nueva técnica que se precie, su cotilleo y su polémica.
Parece claro y aceptado que fue Richard Buckminster Fuller el que acuñó por primera vez el término Tensegrity (Tensegridad) y que fue el primero, en 1959, en registrar una patente de este tipo.
Sin embargo, o por lo menos así lo insinúan muchas fuentes, entre otros el propio Connelly, el primero que construyó una estructura tenségrica fue Kenneth Snelson durante el periodo que fue estudiante suyo, sólo que Fuller fue más rápido en publicar y registrar la patente.
Eso sí, con la cúpulas geodésicas, como la de Montreal al principio de esta entrada, el que se lo ‘curró’ más fue Fuller.
No fue el inventor de las mismas porque ya habían sido utilizadas anteriormente por otros, como el ingeniero alemán Walther Bauersfeld,

o nuestro Ingeniero Torroja, abuelo de la ‘Mecana’, en el Mercado de Abastos de Algeciras
Sin embargo, a Fuller se le concedió la patente de la cúpula geodésisca en 1954 (U.S. 2,682,235) y se le atribuye el honor de haber sido el que popularizó la utilización de las mismas.
De hecho, las moléculas de carbono conocidas como fulerenos tomaron su nombre de su parecido con las esferas geodésicas.
Y, bueno, esta idea ha llegado hasta nuestras vidas en forma de tiendas de campaña
Richard Buckminster Fuller, ahora metafóricamente hablando y dejando que la poesía se cuele en esta entrada, siguió los principios de tensegridad en su vida hasta el último momento, el de su propia muerte. Su mujer estaba ingresada en coma en el hospital, muriendo de cáncer y durante una visita en el hospital, él dijo “¡Ella está apretando mi mano”! Murió una hora después de un ataque al corazón. Su mujer lo hizo 36 horas más tarde. O nos movemos todos o no se mueve nadie…
En cuanto a Snelson, escultor y fotógrafo, aparte de que muchos dedos lo señalan como el verdadero creador de las estructuras de tensegridad, ha sido más prolífico que Fuller en el diseño y construcción de las mismas. Basta un paseo por su página para deleitarse con las imágenes
[youtube]http://www.youtube.com/watch?v=x_pZ-m6Ppyg[/youtube]
o para aprender sobre contrucción de estructuras de tensegridad.
En el siguiente vídeo se puede ver parte del proceso de construcción de una de sus obras.
[youtube]http://www.youtube.com/watch?v=Rd-SuVFHAUU[/youtube]
Y si la idea de la cúpula de Fuller inspiró soluciones para acampadas, las de Snelson han servido para dieñar, también juguetes
Otros nombres vinculados al nacimiento de la tensegridad son Karl Ioganson, artista letón padre de la tensegridad, según el artista ruso Viatcheslav Koleichuk. Sólo que su obra fue destruida por el regimen soviético en los años 20 del pasado siglo. O Alexander Calder, al que el ya mencionado Miguel de Guzmán, señalaba como precursor de la misma con sus esculturas móviles.
Aparte de las aplicaciones artísticas, arquitectónicas o lúdicas, que siempre vienen bien, están los estudios que, por ejemplo, sobre el citoesqueleto, se basaron en relacionar éste con estructuras de tensegridad, principalmente a partir de los trabajos de Donald Ingber( para el que la célula no es una ‘mancha’ son que tiene una estructura de tensegridad en la que la tubulina es el componente rígido y la actina es el componente de tensión, el cable.) y de los que la NASA se hace eco, con la preocupación de qué pasará con las estructuras de las células en ausencia de gravedad.
Según el Dr. Ingber, la tensegridad la podemos usar para interpretar en nuestro cuerpo, a nivel macroscópico en tanto y en cuanto, nuestros huesos (elementos de compresión) se mantienen erectos en contra de la gravedad gracias a la tensión de músculos y tendones (elementos de tensión).
Y a nivel celular, como interpretación de la estructura del citoesqueleto. En su trabajo The architecture of life, nos cuenta como hasta finales de los años 70 del pasado siglo XX, la mayoría de los biólogos explicaban la estructura de la célula como una membrana rodeando a un gel o fluido viscoso. Pero las células tienen una estructura interna, el citoesqueleto, formada por proteínas (microfilamentos, filamentos intermedios y microtúbulos) que pueden podría explicarse con los conceptos que estamos tratando en esta entrada de compresión y tensión, de tensegridad.
A Donald Ingber le llamaba poderosamente la atención, el hecho de que las células aisladas adoptaban formas distintas dependiendo de la superficie en la que estuvieran: éstas se aplanaban en contacto con cristal o placa de plástico, pero se volvían esféricas al contacto con goma, como mostró en 1980 Albert K. Harris. Ingber diseñó una célula como una estructura de seis varillas de madera y cuerda elástica para probar su teoría de que la tensegridad podría interpretar el funcionamiento del citoesqueleto.
Como se ve en la figura superior, el modelo de Donald Ingber, se volvía más esférico si, por ejemplo, la superficie en la que estaba apoyado se arrugaba.
Recomiendo al lector interesado el trabajo de Ingber, ya mencionado en esta entrada en el que explica cómo llegó a la conclusión de la existencia de una tensegridad que explicaba el funcionamiento del esqueleto de la célula. Las implicaciones potenciales de esta investigación son enormes y podría ofrecer nuevos tratamientos para osteoporosis, enfermedades cardíacas, problemas pulmonares y anormalidades en el desarrollo. Cada tejido del cuerpo, dice Ingber, puede desarrollar una enfermedad como consecuencia de una respuesta anormal de las células a fuerzas mecánicas externas.
Arquitectura, escultura, biología, cremas de belleza, ‘magufada’… ¿qué hace una chica como tú en un sitio como éste? O ¿qué tiene que ver esto con matemáticas y teoría de grafos?
Desde el punto de vista matemático, han sido varias las definiciones de estabilidad las que se han estado y se están manejando en el estudio de las tensegridades: rigidez infinitesimal, rigidad estática… Todas estas definiciones están en este trabajo de Connelly y Whiteley Y todas ellas han sido y son objeto de estudio.
Y, efectivamente, el estudio de la tensegridad está intimamente relacionado con el estudio de la Teoría de Grafos como nos explica mi colega y amigo David Orden en este trabajo.
¿Qué es una tensegridad para los de Teoría de Grafos?
Un grafo es un par de conjuntos G =(V;E) para el que los elementos de V se denominan vértices y los elementos de E, denominados aristas, son pares de elementos de V.
Un armazón es una inmersión G(P) de un grafo G, sobre un conjunto de puntos P en el plano o en el espacio, en realidad en cualquier espacio Rd, con segmentos rectos como aristas.
Una auto-tensión en un armazón es una asignación de tensiones wij a las aristas ij, de forma que cada vértice está en equilibrio, es decir, la resultante de las tensiones incidentes a él es nula.
Llamaremos tensegridad a un armazón dotado de una auto-tensión.
Dados un grafo G, ¿puede existir una tensegridad con esa estructura en R3?
O dicho de otra forma, si dibujamos cualquier grafo, ¿podremos construir una estructura con cables, tirantes y barras que lo represente? Poor ejemplo, el grafo de la figura siguiente, ¿podría ser una tensegridad en el espacio tridimensional?
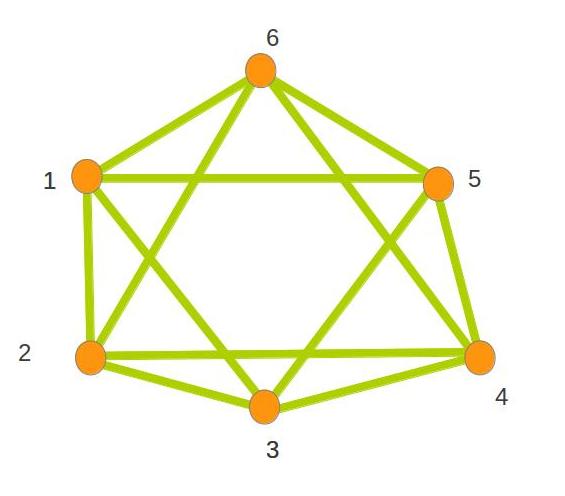 La respuesta es sí como se ve en el trabajo ya mencionado de Orden
La respuesta es sí como se ve en el trabajo ya mencionado de Orden
Ésta y otras preguntas han dado y están dando mucho trabajo a los expertos en teoría de grafos que trabajan en el tema, entre los que cabe destacar los trabajos del ya mencionado Miguel de Guzmán, y, por supuesto, los del mencionado Bob Connelly. Éste último, junto con Bob Terrell tiene una página muy interesante con FAQs sobre tensegridad aquí.
Lo dejamos por aquí, peso si te ha interesado el tema, puedes bucear durante muchas leguas a través de contenidos que implican el concepto de tensegridad.
Y si os interesa mucho, en Zazzle podéis conseguir una camiseta como ésta que fue la que me inspiro el título ¡de esta entrada.
Y hasta aquí, nuestro tira y afloja con la Tensegridad, por ahora…
Referencias:
http://www.angelfire.com/ma4/bob_wb/tenseg.pdf
http://es.scribd.com/doc/46550301/Mathematics-and-Tensegrity
Tensegridades: arte en equilibrio de David Orden
http://tensegrity.wikispaces.com/
The architecture of Life de Donald Ingber
Y todas las que aparecen enlazadas en el texto de esta entrada.
Soy profesora del área de Matemática Aplicada de la Universidad de Sevilla desde un maravilloso día soleado de Noviembre de 1995. Desde entonces he descubierto que la satisfacción de investigar es sólo comparable a la de contar y enseñar lo que has descubierto. Durante más de 10 años esto último se redujo al ámbito de mis clases en la Universidad y a las comunicaciones en congresos. Con la llegada de mis enanos se me planteó el reto de contarlo fuera del aula, en la alfombra del salón. Y oye, me gustó. Ahora dedico parte de mi tiempo libre a la divulgación, para niños de 9 a 99 años, consciente de que a todo el mundo le gustan las matemáticas, solo que algunos aún no lo saben. Mis coordenadas en: claragrima.com.























