No diré eso de – Como decíamos ayer – porque está muy manido, así que sigamos directamente con el tema de los monopolos.
 Hoy enfrentaremos a eso que tanto le gusta a los físicos, eso del – ¿Qué pasaría si? -. Basta con que le digas aun físico que algo es imposible para que busque cualquier forma para demostrar que es imposible que no sea posible. Este paseo lo haremos de la mano del amigo Paul Adrien Maurice Dirac. Dirac es uno de los gigantes de la física, uno de los padres de la mecánica cuántica, el artífice de la transición a la teoría cuántica de campos que consiguió unir relatividad especial y mecánica cuántica de forma consistente, el padre de la antimateria y un larguísimo etc.
Hoy enfrentaremos a eso que tanto le gusta a los físicos, eso del – ¿Qué pasaría si? -. Basta con que le digas aun físico que algo es imposible para que busque cualquier forma para demostrar que es imposible que no sea posible. Este paseo lo haremos de la mano del amigo Paul Adrien Maurice Dirac. Dirac es uno de los gigantes de la física, uno de los padres de la mecánica cuántica, el artífice de la transición a la teoría cuántica de campos que consiguió unir relatividad especial y mecánica cuántica de forma consistente, el padre de la antimateria y un larguísimo etc.
Pues bien, el bueno de Dirac, se empeñó en estudiar qué pasaría si existieran los monopolos. En esta entrada discutiremos, muy pictóricamente, las ideas que llevaron a Dirac a considerar la existencia de esos imposibles y las consecuencias tan inesperadas, sorprendentes e interesantes que extrajo, esas que han traído de cabeza a generaciones enteras de físicos.
Esta entrada es la continuación de: Monopolos, never ending story – Parte I
Corriente eléctrica y campo magnético
Uno de los milagros del electromagnetismo es que aún no existiendo, en primera instancia, las fuentes fundamentales del magnetismo, los monopolos, sabemos que los campos magnéticos sí pueden ser generados por corrientes eléctricas. Este hecho fue puesto de manifiesto por primera vez por Oersted que observó como una corriente eléctrica desviaba la aguja de una brújula. Aquí tenéis un vídeo explicativo, en caso de que haga falta una constatación visua,l de lo que estoy comentando:
[youtube]http://www.youtube.com/watch?v=h5N2grjG8d8[/youtube]
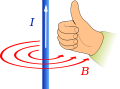
Una visualización de las líneas de campo magnético producidas por un conductor rectilíneo por el que circula una corriente es la siguiente:
Las líneas de campo son circunferencias cerradas centradas en el conductor. (Vuelven a salir líneas cerradas — Insertar enlace entrada anterior—). El sentido de las líneas se puede calcular con la regla de la mano derecha, donde rodeamos el conductor con los dedos de la mano derecha excepto por el pulgar que apunta en la dirección de la corriente eléctrica que circula por el cable:
El solenoide
Hay una configuración de conductor eléctrico muy interesante, el cable conductor se enrolla en forma de espiral, a esto se le llama, solenoide:
 Lo interesante de los solenoides para el tema que nos ocupa es lo siguiente:
Lo interesante de los solenoides para el tema que nos ocupa es lo siguiente:
- Cuando circula una corriente eléctrica por el solenoide se crea un campo magnético como en cualquier otro conductor con corriente.
- El campo magnético tiene una configuración de líneas muy interesante. Es uniforme en el interior del solenoide y en el exterior las líneas se abren de forma que salgan por un extremo (polo norte) y entren por el otro extremo (polo sur).
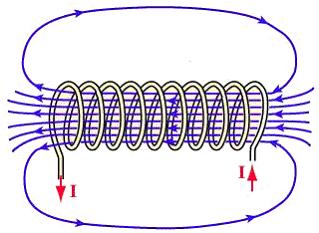 Todas las líneas que salen vuelven a entrar, están condenadas a ello por las ecuaciones de Maxwell.
Todas las líneas que salen vuelven a entrar, están condenadas a ello por las ecuaciones de Maxwell.
¿Por qué es esto tan interesante?
Hagamos un pequeño ejercicio de abstracción. Supongamos que tenemos un solenoide que podemos hacerlo tan largo como queramos, de hecho lo podemos hacer infinitamente largo. Además, podemos hacerlo todo lo delgado que queramos. Así, puestos a abstraernos supongamos que uno de los extremos del solenoide lo llevamos al infinito y que en el proceso hemos reducido su anchura hasta el límite de que sea una única línea. ¿Qué es lo que veríamos en esta situación?
Lo que veríamos es que de un punto emerge un campo magnético con líneas salientes abiertas (buscan a su polo sur asociado pero este está en el ¡INFINITO!). Tenemos que recordar que el otro extremo ha sido enviado al infinito y que la anchura del solenoide se ha llevado al límite de ser una línea. A esa línea, (que tiene particularidades matemáticas como la de venir descrita por una singularidad del potencial vector) se la denomina cuerda de Dirac y está asociada a la presencia de un monopolo creado con este procedimiento.
Nota: Podéis ver una serie de vídeos explicativos sobre todos estos temas pinchando AQUÍ. Estos vídeos se crearon para explicar la búsqueda de los monopolos magnéticos en el experimento MoDEAL del CERN.
El problema con esta imagen de un monopolo, que es bastante natural (es un simple ejercicio de abstracción), es que la dichosa cuerda de Dirac que estaría asociada con cualquier monopolo no debe de ser observable directamente. Y para que eso ocurra se tienen que cumplir algunas cosas:
- Supongamos que nuestro monopolo tiene una carga magnética de un valor que representaremos por g.
- Supongamos que tenemos un mínimo de carga eléctrica que coincide con la carga del electrón en valor absoluto (la carga del protón) y que representamos por e.
Dirac llegó a la conclusión de que:
,
donde es un número entero.
Si se cumple esta relación Dirac nos asegura que su cuerda (asociada a su monopolo) es inobservable lo que es una característica deseable. Y lo que es más, las cargas eléctricas no interactuarían más que con el campo magnético generado por el monopolo pero no sentirían el que está confinado dentro de la cuerda de Dirac.
Ahora nos podríamos preguntar, ¿y esto que tiene de espectacular?
Lo que tiene de espectacular es que es bien conocido que las cargas eléctricas siempre se presentan como múltiplos enteros de la carga del electrón (con signo positivo o negativo), es decir, la carga está discretizada y no podemos tener cargas fraccionarias enteras o irracionales de la carga del electrón. En la época de Dirac no se tenía ninguna explicación de este hecho, pero observemos qué pasa al reescribir la anterior expresión de la siguiente manera:
Es decir, que si existen monopolos con un valor de carga g apropiado, las cargas eléctricas solo se presentarían como múltiplos enteros de una determinada cantidad, (en valor absoluto, para obviar signos), que depende de la carga magnética del monopolo. A esta relación, de hecho a la anterior, se la conoce como condición de cuantización de Dirac.
Conclusiones
Dirac mostró que era posible incorporar, por la puerta de atrás, monopolos a la teoría del electromagnetismo. Además con ello consiguió dar cuenta de por qué las cargas eléctricas siempre aparecen como múltiplos enteros de una carga fundamental (la carga del electrón en valor absoluto).
Sin embargo, en su fuerza encontramos su debilidad. Esta construcción se puede considerar demasiado artificial y eso es algo que en física desagrada mucho. Pero la historia no se para aquí, la última palabra aún está por escribirse y nos quedan unos cuantos pasos más en este cuento de los monopolos magnéticos. Hoy día, se considera que estos bichos tienen que existir de manera natural siempre que se den unas cuantas condiciones de las que daremos buena cuenta en breve. Por lo que parece, los monopolos podrían estar mirándonos escondidos detrás de alguna de las cortinas de la física. Insistiremos en ello en próximas entregas.
Nos seguimos leyendo…
————————-
Este post es tan solo uno de los cinco artículos de la serie de Enrique F. Borja dedicada a los monopolos magnéticos, puedes encontrar la serie completa en:
Monopolos, never ending story – Parte 1
Monopolos, never ending story – Parte 2
Monopolos, never ending story – Parte 3
Monopolos, never ending story – Parte 4
Monopolos, never ending story – Parte 5
Intento escribir sobre física. A veces lo he conseguido.
Me parece importante remarcar que creo en cosas que no he visto, por ejemplo, en los electrones. También tengo varios diplomas, del que más orgulloso me siento es el de participante en la Olimpiada Infantil de 1992; nos dieron un bocata de salchichón y una camiseta.