Bueno, hemos llegado al final de esta historia contada a trozos:
Monopolos, nerver ending story: Parte 1, Parte 2, Parte 3 y Parte 4.
Hemos visto como los monopolos, en principio, no tienen cabida en el electromagnetismo. Luego vimos que se pueden introducir en la física siguiendo el método «heurístico» de Dirac y tras ello nos hemos ido por las ramas para hablar de teorías gauge, simetrías rotas y configuraciones de erizo en los campos situados en el espaciotiempo.
Es hora de poner en contexto las dos últimas entradas y entender por qué hemos «perdido» el tiempo con estas cuestiones gauge y de rotura de simetrías cuando lo que nosotros queríamos era hablar de monopolos magnéticos y su posible existencia. Empecemos…
Los erizos que encierran monopolos
 En la entrada anterior vimos que una de las posibles configuraciones de un campo en el que hemos roto la simetría desde SO(3) a U(1) para pasar a su vacío es la denominada configuración del erizo.
En la entrada anterior vimos que una de las posibles configuraciones de un campo en el que hemos roto la simetría desde SO(3) a U(1) para pasar a su vacío es la denominada configuración del erizo.
Esta configuración la podemos entender como sigue:
1.- El campo está en su estado de vacío, estado de mínima energía, y eso lo vemos en que su módulo tiene un determinado valor en todo el espacio. Ese valor se considera la masa del campo (de sus partículas asociadas según el entendimiento de los campos que tenemos en cuántica).
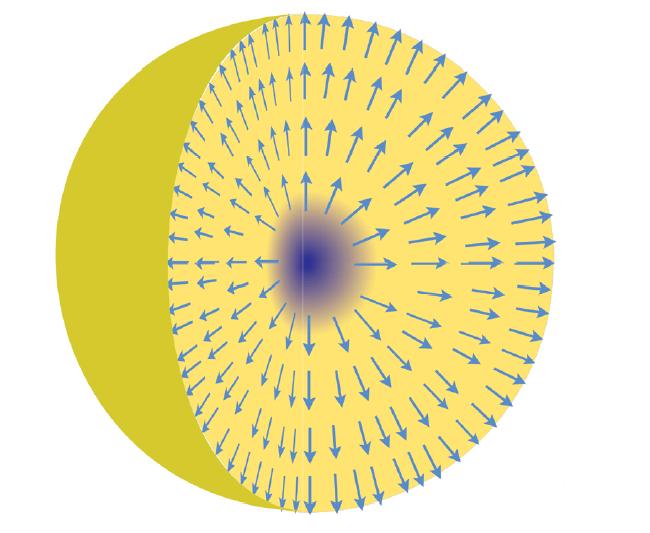
2.- Una de las configuraciones es la del erizo, donde los vectores del campo (con módulo fijo correspondiente al vacío del campo) describen una esfera.
 Esta situación es singular, ¿qué significa eso?
Esta situación es singular, ¿qué significa eso?
a) Elige una dirección, el campo estará apuntando hacia afuera de la esfera que define.
b) Muévete en dicha dirección hasta que pases por el centro de dicha esfera y sigue avanzando. Notarás como cualquier vector del campo apunta en el sentido opuesto al que has empezado. Observa la siguiente figura:
3.- Esto solo se puede dar si en el centro el campo definido en esos puntos del espaciotiempo tiene un módulo nulo. Es decir, hay una situación que tenemos que cambiar de sentido vectores del mismo módulo pasando por un punto donde los vectores tienen que tener módulo nulo.
¿Pero qué ocurría cuando el módulo del vector era nulo? Pues ocurría que estaba en su estado de falso vacío, el campo tenía una energía no mínima y tenía una simetría SO(3).
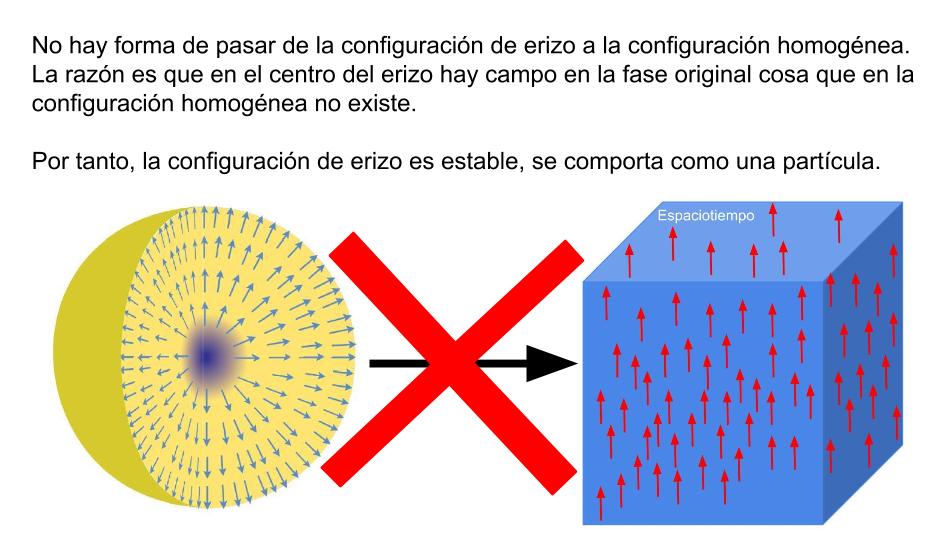
Eso implica que esta configuración protege un «núcleo» donde el campo permanece en su estado inicial con la simetría inicial. ¿Te parece raro? Mira esta figura:
 En los cubos de hielo siempre se observan fracturas, burbujas, defectos en definitiva en los que hay agua encapsulada. Es decir, en la transición de fase que nos lleva desde el agua líquida al hielo siempre se dan defectos en los que el sistema conserva partes en la fase inicial. Este hecho es justamente el análogo al que estamos discutiendo aquí con el campo en la configuración del erizo. El campo encapsula su fase original por una distribución específica del campo en la nueva fase.
En los cubos de hielo siempre se observan fracturas, burbujas, defectos en definitiva en los que hay agua encapsulada. Es decir, en la transición de fase que nos lleva desde el agua líquida al hielo siempre se dan defectos en los que el sistema conserva partes en la fase inicial. Este hecho es justamente el análogo al que estamos discutiendo aquí con el campo en la configuración del erizo. El campo encapsula su fase original por una distribución específica del campo en la nueva fase.
Estos defectos tienen energía y de hecho son estables. Son estables porque no hay forma natural de deshacer esta configuración de erizo de forma continua. Uno no puede pasar de esa configuración de erizo a una configuración homogénea del campo (precisamente porque hay regiones de fase original del campo).
Así que, eso que hemos llamado erizo se comporta de forma estable, no se disipa, una vez formado tiene una estructura que se mantiene y evoluciona como una partícula.
Esto es importante, ¿por qué?
Pues porque hemos dicho que en teoría cuántica de campos todo campo tiene partículas asociadas. Eso ocurre al introducir las reglas cuánticas en las teorías que describen los campos físicos. Sin embargo, hay otro tipo de partículas que hemos descubierto, estas están relacionadas con la configuración que toma un campo tras una rotura de simetría, no aparecen como una cuantización del campo en sí mismo.
¿Qué son esas partículas?
Esas partículas a las que nos estamos refiriendo tienen propiedades electromagnéticas, recordemos que están recubiertas de campos con simetrías U(1) que implicaba la existencia del electromagnetismo. Lo sorprendente es que si calculamos el campo electromagnético que produce una partícula de esas nos dirá que para un observador en reposo respecto a la misma esta partícula produce el campo magnético asociado a un monopolo. Por lo tanto, son monopolos.
¿Existen estos monopolos?
Esto que hemos explicado en estas entradas no es extrapolable al modelo estándar de las partículas elementales. Solo tiene sentido esta explicación si nuestras partículas tienen espacios internos asociados tal que su rotura produzca un espacio interno U(1) cosa que no ocurre en el modelo estándar. ¡Vaya!, pues parece que sí hemos perdido el tiempo, o tal vez no.
Actualmente los físicos están convencidos de que todas las interacciones, electromagnetismo, débil y fuerte, estuvieron unificadas en un único esquema teórico, teoría de gran unificación, al principio del universo. Esto quiere decir que los campos, cuando el universo era muy joven, veían un espacio interno diferente del que ven ahora, el del modelo estándar, y esto se produce por roturas de la simetría.
Pues bien, resulta que todos los esquemas de gran unificación conocidos tienen un mecanismo de rotura de simetría idéntico, cualitativamente hablando, que el que hemos descrito en estas entradas. Eso implica que los monopolos son una consecuencia ineludible de las teorías de gran unificación.
¿Dónde están los monopolos?
Si creemos que nuestras interacciones originalmente estaban unificadas y eso implica que los monopolos han de existir sí o sí, ¿dónde están dichos monopolos? ¿Por qué no los hemos detectado aún?
La respuesta no es trivial, en todos los esquemas de gran unificación que suponemos viables aparecen los monopolos, eso es cierto. Pero también es cierto que no los hemos visto nunca. Además, los modelos de gran unificación predicen que cuando su simetría se rompe, dando lugar a la del modelo estándar, se crean muchos monopolos. Las predicciones más groseras nos dicen que tendría que haber en el universo tantos monopolos como fotones, y eso no es correcto.
Eso supuso un problema en cosmología por dos motivos:
a) El número de monopolos que se originarían en la rotura de simetría de gran unificación era muy alto y no los vemos.
b) La masa calculada de dichos monopolos es muy elevada. De hecho es tan elevada que hubieran provocado que la gravedad que producían hubiera recolapsado al universo nada más nacer por lo que no podría haber evolucionado hasta nuestros días.
La solución a este problema la dio Alan Guth, el universo sufrío un proceso de expansión muy, muy grande en un corto intervalo de tiempo, la inflación cosmológica. Esta expansión se produjo justo en el momento de producirse los monopolos, con lo que cuando se estaban creando la inflación los separaba distancias tremendas con lo que su densidad en la actualidad, predice la teoría inflacionaria, debe de ser despreciable. Así que, no ver monopolos respalda la idea de la inflación (este fue el motivo inicial de introducir la inflación cosmológica que hoy día cada vez tenemos más comprobada observacionalmente).
¿Se están buscando los monopolos fundamentales?
Sí, hay varios experimentos que están planteados para encontrar estas partículas y aunque no consigan encontrarlas el hecho de buscar y no encontrar introducirá límites en su densidad y en su comportamiento.
Si te preguntas si se pueden producir monopolos en los aceleradores como el LHC la respuesta es no, la energía de estos aceleradores no es suficiente para crear monopolos fundamentales ya que su masa es muy alta.
Daremos algunas referencias sobre experimentos de observación, directa o indirecta, de monopolos:
Introduction to magnetic monopoles
Theoretical and experimental status of magnetic monopoles
Conclusiones
El estudio de monopolos magnéticos es muy interesante. Su existencia implica una sorpresa a nivel físico y una sorpresa a nivel matemático.
Desde el punto de vista matemático los monopolos deben su existencia a razones topológicas. Para estudiarlos de forma adecuada hay que introducir conceptos como grupos recubridores, grupos de homotopía, grupos semisimples de Lie, invariantes topológicos, lema de Poincaré, teorema de Atiyah-Singer, etc.
Unas cuantas referencias para profundizar en el tema:
Introduction to magnetic monopoles – Arttu Ranjatie (2012)
Introducción amena y no técnica del tema que hemos tratado en estas entradas. Muy recomendable.
Monopoles, Instantons and Confinement – Gerard ‘t Hooft (2000)
Discusión de monopolos por parte de uno de sus padres (en la versión actual). Indispensable aunque muy técnica.
Magnetic monopoles in gauge theories – Goddard y Olive (1978)
Un clásico indispensable. Con gran profusión del tratamiento matemático.
Y para ver el origen de la inflación cosmológica y su relación con la ausencia de monopolos – Artículo de Alan Guth, sección IV.
Espero que os haya interesado el tema y haber sabido transmitir la idea de que los monopolos deberían de existir. Continuaremos buscando.
Nos seguimos leyendo…
————————-
Este post es tan solo uno de los cinco artículos de la serie de Enrique F. Borja dedicada a los monopolos magnéticos, puedes encontrar la serie completa en:
Monopolos, never ending story – Parte 1
Monopolos, never ending story – Parte 2
Monopolos, never ending story – Parte 3
Monopolos, never ending story – Parte 4
Monopolos, never ending story – Parte 5
Intento escribir sobre física. A veces lo he conseguido.
Me parece importante remarcar que creo en cosas que no he visto, por ejemplo, en los electrones. También tengo varios diplomas, del que más orgulloso me siento es el de participante en la Olimpiada Infantil de 1992; nos dieron un bocata de salchichón y una camiseta.