Hoy nos toca hablar sobre la rotura espontánea de la simetría. Este es un tema extenso e interesante que ha sido muy aireado en todos los foros, blogs y publicaciones científicas debido a su papel preponderante en el mecanismo de Higgs, ese que da masa a algunas partículas fundamentales y que ha estado de moda debido al descubrimiento del bosón de Higgs en el LHC.
Lo que pretendo es introducir el tema de la rotura espontánea de la simetría, lo haré con la intención de acabar mostrando que los monopolos magnéticos pueden aparecer de forma natural en las teorías gauge (con determinadas características) que sufren este proceso de rotura espontánea de la simetría. Este resultado fue establecido independientemente por t’ Hooft y por Polyakov en 1974. Sus implicaciones las discutiremos en la próxima entrada que será la última de esta saga.
Permitidme un consejo, sería interesante tener frescas las entradas anteriores de esta serie ya que vamos a recurrir a terminología e ideas introducidas en ellas. (Especialmente la tercera entrada de este ciclo es esencial para poder entender lo que aquí vamos a presentar).
Monopolos, nerver ending story: Parte 1, Parte 2, y Parte 3.
Simetría en los espacios internos
Supongamos que tenemos un campo en el que el espacio interno que porta (en cada punto del espaciotiempo) es una esfera. La esfera, por precisar, solo hace referencia a la superficie esférica, está hueca, solo es eso, la superficie. A este espacio interno lo llamaremos, por ser consistentes con físicos y matemáticos, SO(3). Así que, a todos los efectos, cuando digamos SO(3) nos referiremos a que el espacio interno que estamos considerando es una esfera.
Este espacio interno tiene una simetría clara, podemos girar una esfera como queramos, el ángulo que queramos y en la dirección que queramos, y seguirá siendo igual, indistinguible de la situación original. Así que, si nos pusiéramos serios, lo que querríamos construir es una teoría física que permaneciera invariante cuando hiciéramos rotaciones de la esfera SO(3).
Veamos todo esto en imágenes:

Ahora podremos comprobar, aunque estoy seguro que hace falta, que este espacio es invariante bajo rotaciones:
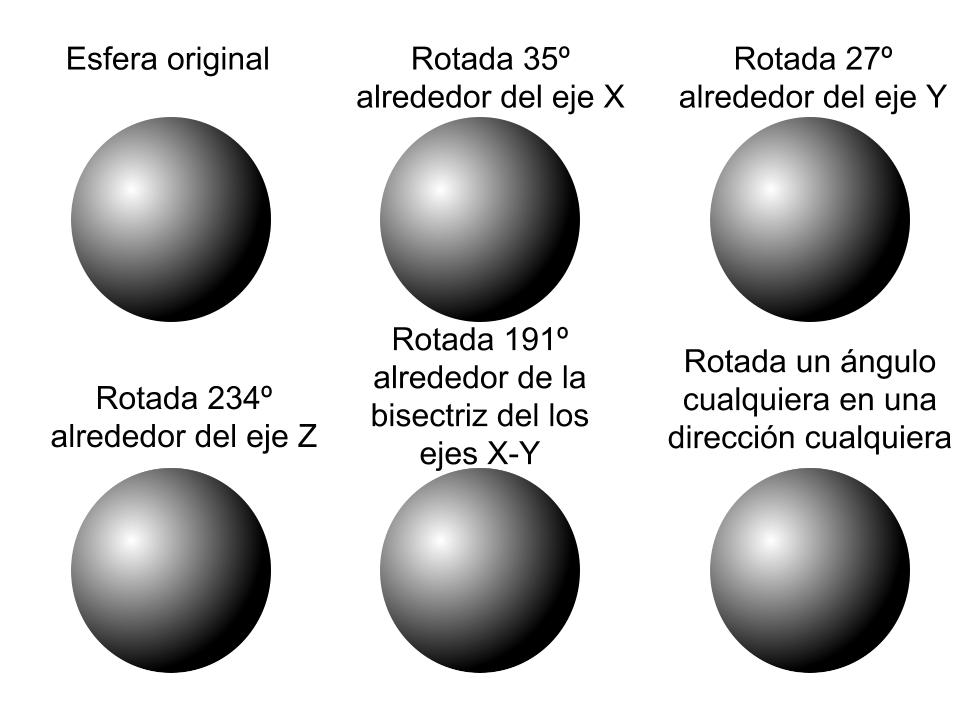 Se ve que cualquiera de las rotaciones deja igual a la esfera. No podemos distinguir un caso de otro, a eso se refieren los físicos cuando hablan de las simetrías, son las simetrías de los espacios internos.
Se ve que cualquiera de las rotaciones deja igual a la esfera. No podemos distinguir un caso de otro, a eso se refieren los físicos cuando hablan de las simetrías, son las simetrías de los espacios internos.
Ahora supongamos que por algún motivo, elegimos un vector que va desde el centro de la esfera hasta su superficie. Esto hace que la simetría de SO(3) se rompa, en este caso sí podremos distinguir distintas situaciones para distintas rotaciones:
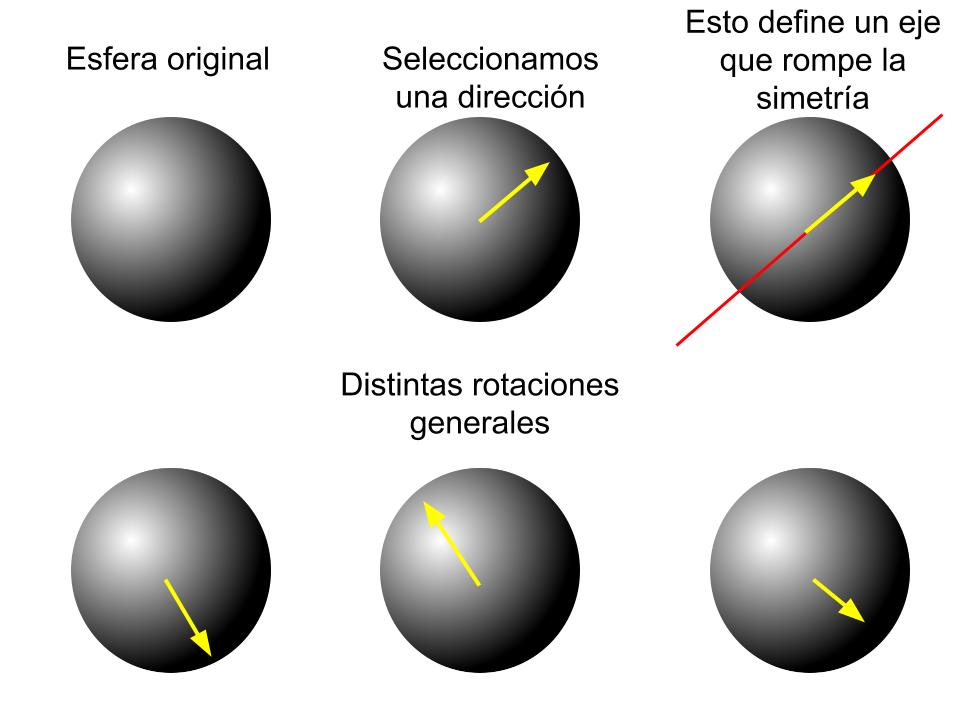 Vaya, la simetría se ha roto por haber seleccionado una dirección de todas las inicialmente posibles y simétricas.
Vaya, la simetría se ha roto por haber seleccionado una dirección de todas las inicialmente posibles y simétricas.
Quien tuvo, retuvo
¿Qué pasa cuando se rompe una simetría? Pues generalmente, el sistema retiene algo de la simetría original, no completa pero sí en parte. Esto quedará claro con el ejemplo que estamos tratando. Inicialmente tenemos un espacio interno que es una esfera (SO(3)), elegimos una dirección privilegiada (los motivos de esta elección privilegiada y arbitraria vendrán después) y eso rompe la simetría. Pero observemos mejor lo que ocurre:
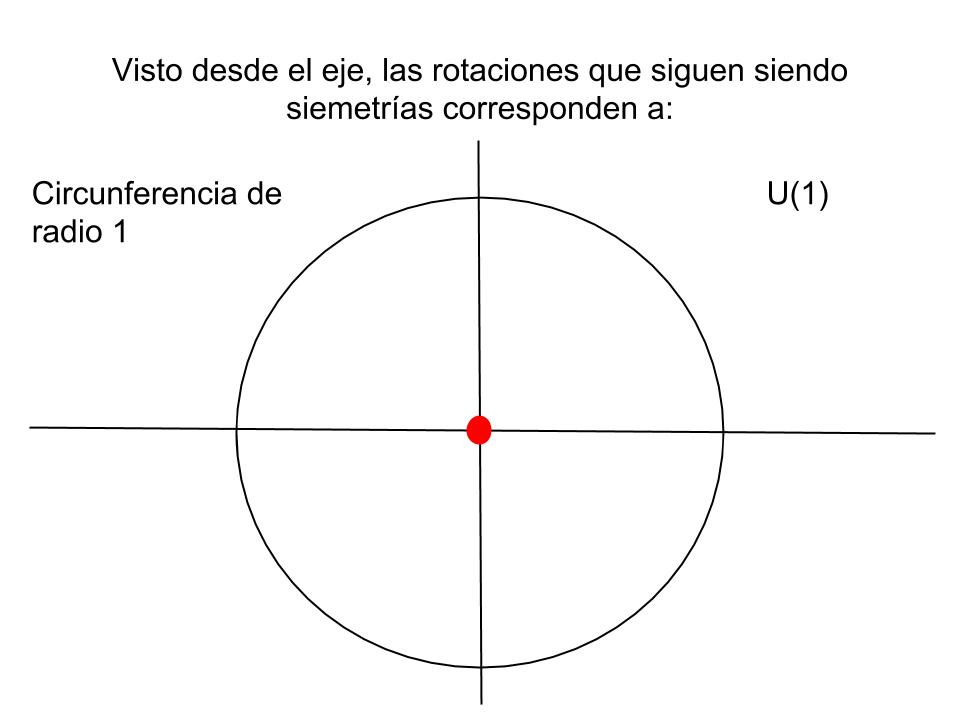
 Si restringimos las rotaciones admisibles en la teoría a aquellas alrededor del eje que ha sido seleccionado de forma arbitraria, aún tenemos una simetría en el sistema. De hecho podemos observarlo mejor si hacemos el gráfico fijándonos simplemente en la sección perpendicular al eje que pasa por el ecuador de la esfera respecto de dicho eje:
Si restringimos las rotaciones admisibles en la teoría a aquellas alrededor del eje que ha sido seleccionado de forma arbitraria, aún tenemos una simetría en el sistema. De hecho podemos observarlo mejor si hacemos el gráfico fijándonos simplemente en la sección perpendicular al eje que pasa por el ecuador de la esfera respecto de dicho eje:
¡Fantástico! Lo que resulta es que el sistema que inicialmente tiene una simetría correspondiente a un espacio interno de tipo SO(3) al elegir un eje y romperse dicha simetría aún conserva una simetría más pequeña, la rotaciones alrededor de dicho eje. El espacio resultante es el correspondiente a una teoría que tiene simetría U(1). ¡Y ya vimos que si una teoría tiene esa simetría necesariamente tiene que involucrar al electromagnetismo!
¿Qué tiene que ver esto con los monopolos?
Tenemos que dar un par de pinceladas más para poder responder a esta pregunta.
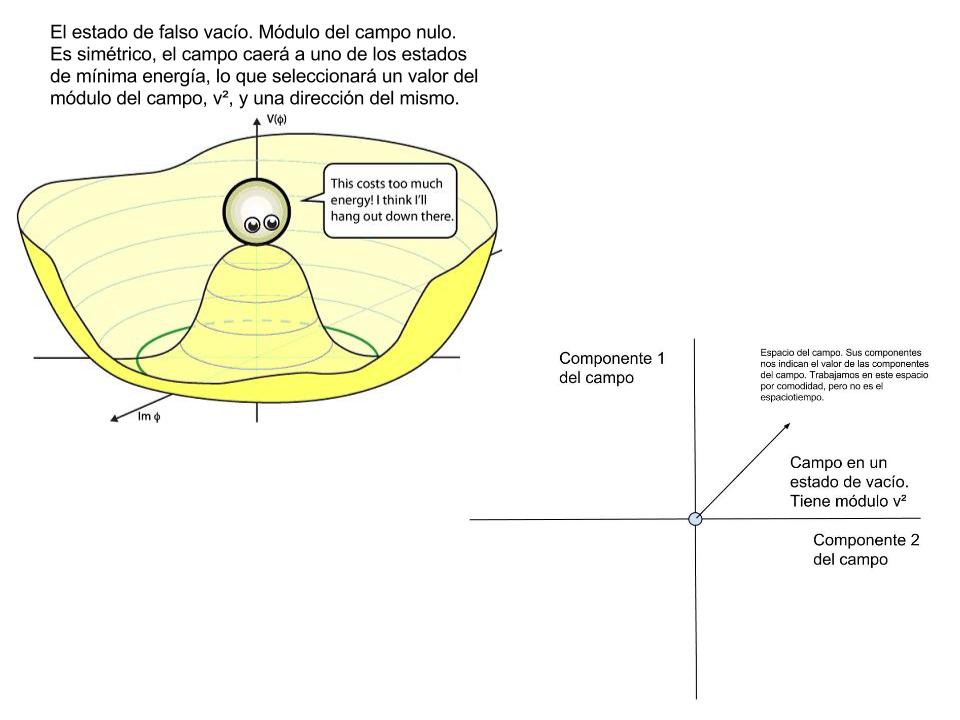
Recordemos que hemos dicho que un campo descrito en términos cuánticos está asociado a la aparición de unas determinadas partículas asociadas (cuyas cargas e interacciones vienen fijadas por las simetrías de sus espacios internos, las teorías gauge). Un estado interesante de todo campo es su estado de vacío. Podemos considerar que el vacío de un campo es su estado de menor energía. Usualmente ocurre que cuando un campo está en su estado de vacío, su estado de menor energía, no hay partículas asociadas a dicho campo presentes. Pero eso no es siempre así.
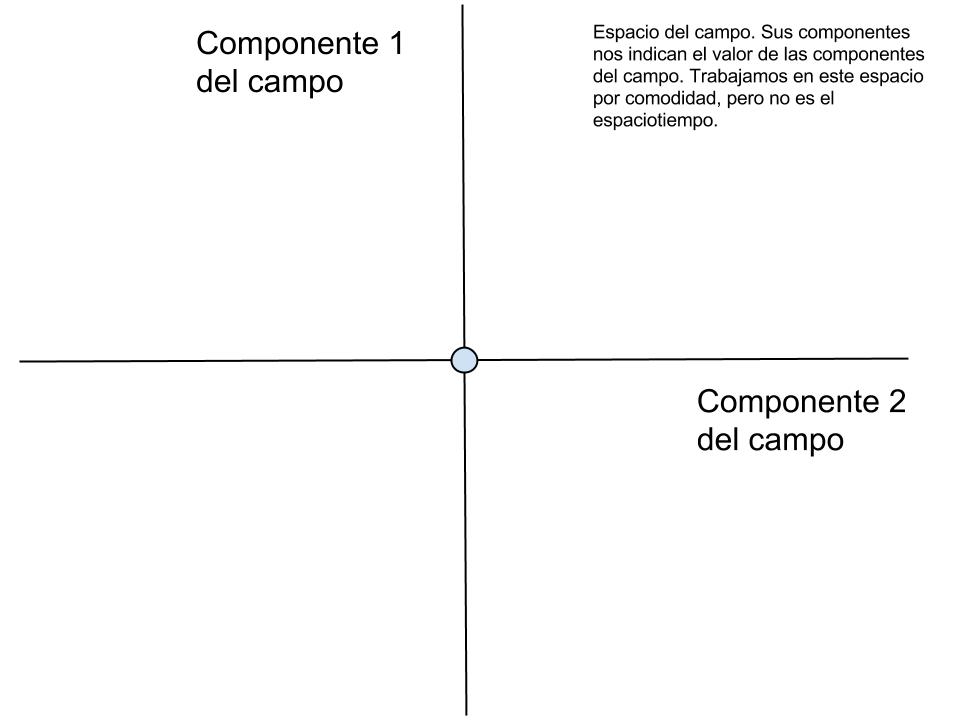
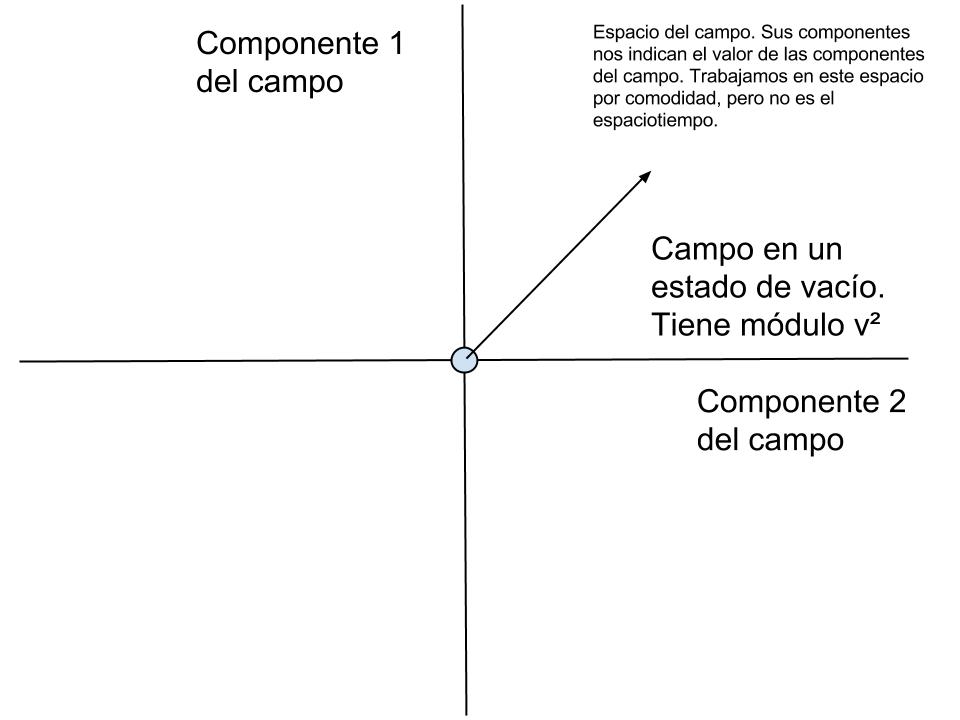
Para no complicar la cosa con partículas y demás, diremos que si representamos el campo en un espacio especialmente construido para él, que no haya partículas asociadas al campo tiene que ver con el hecho de que en dicho espacio artificial (que no es el espaciotiempo) el campo tiene módulo nulo. En cualquier otro estado, el campo representado por un campo de módulo v², indicará que sí hay partículas presentes del mismo y con una masa de las mismas dada por esa cantidad, v².
Como hemos dicho, el campo puede que tenga un estado de mínima energía cuando sí hay partículas presentes del mismo. Dicho de otro modo, en el diagrama que hemos puesto el estado con componentes en el origen no tiene la mínima energía, la mínima energía se alcanza cuando el campo tiene un módulo v².
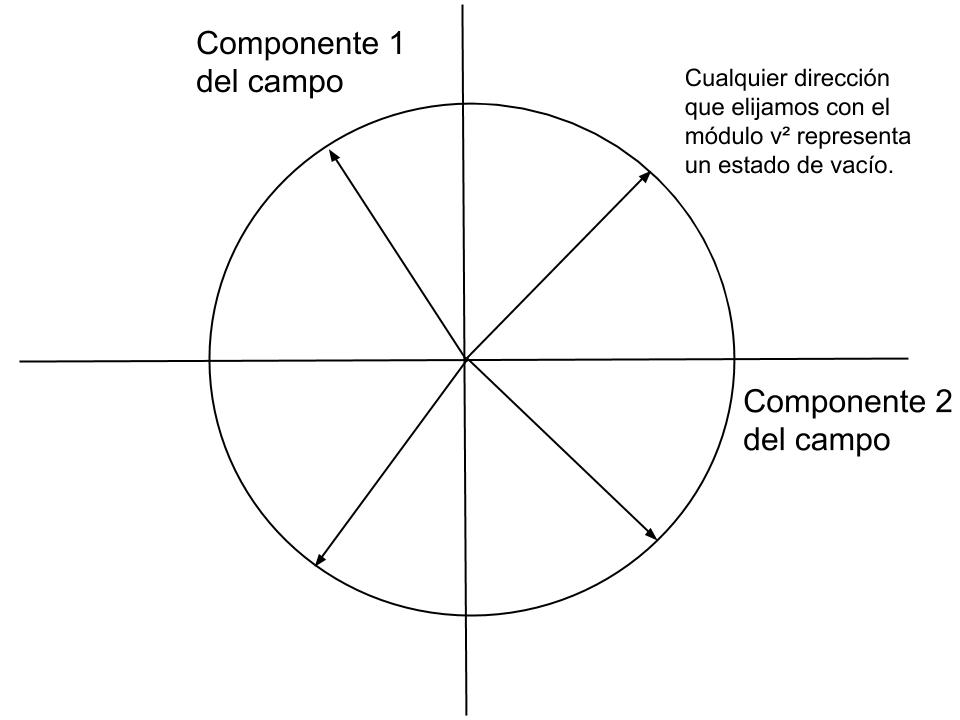
Esta elección que hemos hecho ha sido arbitraria, cualquier vector que represente al campo cuya punta de flecha esté en una circunferencia de radio v² representará al mismo estado de vacío:
Precisemos esto un poco más.
Haremos una representación de la energía del campo para distintos valores de sus componentes, el campo con el que trabajamos, que suponemos que tiene originalmente una simetría SO(3), no tiene un mínimo de energía cuando está en el origen (módulo nulo, también llamado falso vacío del campo) del espacio propio del campo. Así que, como todo sistema tiene una tendencia espontánea a ir a su estado de mínima energía el campo caerá a dicho mínimo y seleccionará de manera arbitraria y espontánea una dirección del campo.
El campo selecciona de forma espontánea una dirección, con lo cual su simetría original SO(3) se rompe a una simetría U(1) como ya hemos explicado. Por lo tanto, un subproducto de la rotura de simetría es la aparición del electromagnetismo que inicialmente no estaba.
¿Y qué pasa en el espaciotiempo?
Todo lo discutido anteriormente se refería a los espacios internos de los campos, es decir, a esos espacios que pueden sondear los campos pero que no están relacionados de forma directa con la posición que ocupan dichos campos en el espaciotiempo. En esta sección vamos a discutir lo que ocurre en el espaciotiempo una vez el campo ha roto la simetría de SO(3) a U(1).
Recapitulemos:
1.- El campo tiene originalmente una simetría interna correspondiente a un espacio SO(3).
2.- Si este campo rompe la simetría de forma espontánea, porque elige un vacío, le queda residualmente una simetría U(1).
3.- El efecto de romper la simetría eligiendo un vacío se traducía en que el campo tenía que ser un vector con un determinado módulo (al que hemos llamado v²).
Para saber qué le ocurre al campo en el espaciotiempo cuando está en su estado de vacío, (recordemos que los campos se definen como sistemas definidos en cada punto del espaciotiempo), tenemos únicamente que pensar que en cada uno de los puntos del espaciotiempo tendremos un vector del campo que únicamente tiene que asegurar que tiene el módulo correspondiente a su vacío. Por lo tanto, tenemos una restricción en el módulo, está fijado en el vacío del campo, pero no en su dirección. Así podemos tener varias configuraciones:
Por ejemplo podríamos tener esta configuración en cada punto del espaciotiempo:
El campo, en el espaciotiempo, está en su vacío (= tiene módulo v², o mejor dicho, su masa es v²) y está distribuido de forma uniforme. Este es el vacío natural en este tipo de teorías. Pero aún hay más…
Podemos tener esta configuración:
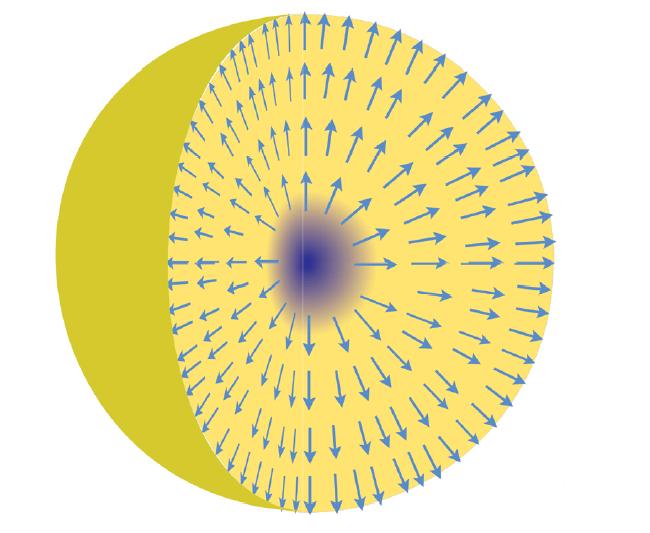 El campo se distribuye en el espaciotiempo de forma radial alrededor de un determinado punto. A esta configuración se la conoce como configuración del erizo. Hay más configuraciones posibles, pero nos vamos a detener en esta que es la que nos interesa 🙂
El campo se distribuye en el espaciotiempo de forma radial alrededor de un determinado punto. A esta configuración se la conoce como configuración del erizo. Hay más configuraciones posibles, pero nos vamos a detener en esta que es la que nos interesa 🙂
Como veremos en la siguiente entrada, esta configuración es la que tiene todas las propiedades de un monopolo magnético, que es a la conclusión que llegaron ‘t Hooft y Polyakov. Pero creo que es mejor dejar reposar todo esto un rato y continuar en otro momento (ya queda menos).
Nos seguimos leyendo…
————————-
Este post es tan solo uno de los cinco artículos de la serie de Enrique F. Borja dedicada a los monopolos magnéticos, puedes encontrar la serie completa en:
Monopolos, never ending story – Parte 1
Monopolos, never ending story – Parte 2
Monopolos, never ending story – Parte 3
Monopolos, never ending story – Parte 4
Monopolos, never ending story – Parte 5
Intento escribir sobre física. A veces lo he conseguido.
Me parece importante remarcar que creo en cosas que no he visto, por ejemplo, en los electrones. También tengo varios diplomas, del que más orgulloso me siento es el de participante en la Olimpiada Infantil de 1992; nos dieron un bocata de salchichón y una camiseta.