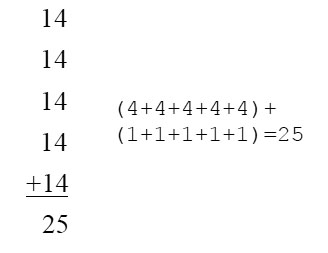O bien eres muy soberbio, o inconsistente.
Prueba:
Tienes un número finito de creencias. A menos que seas muy soberbio, sabes que algunas de tus creencias deben de ser falsas. Pero sigues creyendo en cada una de ellas, de modo que aunque sabes que por lo menos una es falsa, actúas como si todas fuesen verdaderas. Por lo tanto, eres inconsistente.
QED
En un capítulo muy viejo de la serie Dr. Who, su asistente le espeta que su proceder, como de costumbre, no tiene ninguna lógica. El Doctor le contesta, “querido amigo, la lógica no es sino una manera de decir tonterías con aires de autoridad.”
La lógica es una de las armas más potentes del pensamiento: la manera de comprobar que la estructura de nuestras inducciones es consistente; claro que el problema de siempre es partir de premisas equivocadas, así se ha llegado históricamente a muchas salvajadas, pero perfectamente estructuradas.
Además de esa obviedad, existen las falacias: argumentos que parecen tener peso pero que de hecho no lo tienen. La falacia es un tópico de extrema importancia en el estudio de la lógica desde hace más de dos mil años: en tiempos clásicos su aplicación estaba en la retórica y la oratoria pública, así como en la filosofía y la teología. Más recientemente las falacias y otras particularidades ambiguas del lenguaje natural, son materia de estudio en la construcción de inteligencias artificiales (IA) que puedan reconocer sus sutilezas. Hay una larga lista de falacias famosas, conocidas y usadas desde tiempos de Aristóteles: el ataque ad hominem, la petición de principio, el hombre de paja y un largo etcétera. Porque para convencer al otro y usando una herramienta tan fluida como el lenguaje natural, por supuesto que echamos mano de cuanta cosa podamos. Muchas falacias de hecho son usadas sin darnos cuenta de que las usamos, esto es, que no sabemos que estamos usando una falsa argumentación. Como se ha dicho, “no discutimos para aprender, sino para ganar la discusión.” La excepción quizá son los políticos, que saben que nada de lo que dicen es cierto, pero ese tema será para otra ocasión.
Ahora bien, aquí lo que nos ocupa no son las falacias clásicas, que a veces son usadas conscientemente y a veces no. Lo que veremos es un ejemplo de argumento explícitamente tramposo, aplicado a matemáticas. El argumento es muy gracioso y a primera vista es impactante porque no sólo se enuncia, sino que se realiza con un procedimiento completo, esto es, que se muestra la prueba de que es verdad.
Fue usado en dos películas cómicas clásicas: los primeros en presentarlo fueron los inolvidables Abbott y Costello en su película In The Navy (1941), en donde Abbott demuestra más allá de toda duda, que 7 x 13 = 28:
Un argumento parecido es usado en Ma & Pa Kettle Back on the Farm (1951), para demostrar que 25/5 = 14, otra vez de tres formas diferentes:
Método 1.
Preparando la división, Pa dice: “5 no cabe en el 2, así que lo dividimos entre el 5 una vez. (Pone el 1 arriba). Quitamos ese 5 y obtenemos 20. Luego dividimos ese 20 entre 5 otra vez, y obtenemos 4. (Pone el 4 arriba, obteniendo 14).
Ma opta por multiplicar. Primero multiplica 5 x 4 y obtiene 20. Luego multiplica el 5 por el 1 y obtiene 5. Sumando 20 y 5, obtiene 25.
Pa vuelve a demostrar el resultado, ahora con una suma. Es igual al método anterior, pero desglosado: primero se suman explícitamente todos los 4’s, para obtener 20. Luego se suman todos los 1’s para obtener 5, y se vuelve a sumar 20+5.
¿Cómo le explica el lector los 3 errores a un niño que está aprendiendo a multiplicar y dividir?
Referencias:
Smullyan, Raymond M,. What is the Name of this Book?: The Riddle of Dracula and Other Logical Puzzles (Dover Recreational Math). Dover Publications, 2011.
Falacia. Wikipedia.
Argumento ad hominem. Wikipedia.
Petición de principio. Wikipedia.
Falacia del hombre de paja. Wikipedia.
Abbott y Costello, In the navy, 1941. 7*13 = 28
Ma & Pa Kettle Back on the Farm (1951) 25/5 = 14
Nací en México y vivo en China desde el 2000, donde estudié idioma e historia, y luego fui investigador visitante en el Centro Internacional Wan Lin Jiang de Economía y Finanzas, así como profesor de economía e historia para extranjeros en la Universidad de Zhejiang. Actualmente dirijo el Mexico-China Center y doy conferencias acerca de ciencia y cooperación tecnológica internacional.