
10. ROTACIONES Y UNA PARADOJA
Pasemos a un tema que naturalmente emerge de nuestro sistema: las rotaciones. Este tema lo relacionaremos con una de nuestras definiciones: la Extensión X(e) de la escala.
Recordemos que definimos la Extensión como la relación entre el área del Polígono de la Escala vs. el área total del dodecágono. Para abundar, dijimos que esto equivale a decir qué tanto espacio puede la escala abarcar del total de su “potencial tonal”. Si tenemos un polígono con área —o en nuestro vocabulario, Amplitud A(e)— menor, obviamente su Extensión X(e) será menor. También vimos que en varias instancias, el polígono creado por una escala, a medida que cambia su orientación en nuestro espacio, toma nombres de otras escalas conocidas sin alterar su forma.
Llevemos esto a su conclusión lógica: realizar todas las rotaciones posibles del polígono, no solamente las rotaciones a las que fácilmente podemos relacionar con nombres reales de escalas. Por ejemplo: vimos que en nuestra forma clásica de construcción de escalas musicales, obtenemos siete estructuras a partir de la tónica, cada una con su nombre (jónica, dórica, etc.). Si sobreponemos todas estas rotaciones en un solo diagrama, obtenemos:
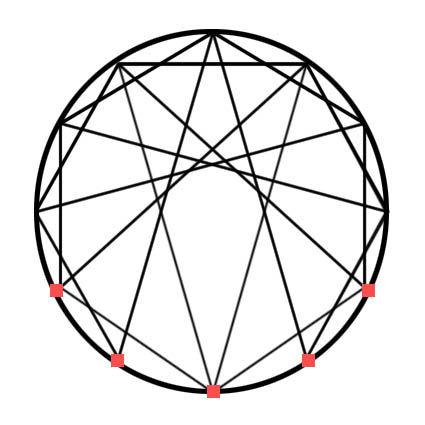 O sea, no es una rotación completa, sino que los cinco puntos en rojo —los más alejados armónicamente de la nota fundamental— se quedan sin usar como punto de orientación. Para nuestros fines geométricos, completemos las rotaciones de las estructuras, superponiendo los resultados en un solo diagrama. Así obtenemos:
O sea, no es una rotación completa, sino que los cinco puntos en rojo —los más alejados armónicamente de la nota fundamental— se quedan sin usar como punto de orientación. Para nuestros fines geométricos, completemos las rotaciones de las estructuras, superponiendo los resultados en un solo diagrama. Así obtenemos:
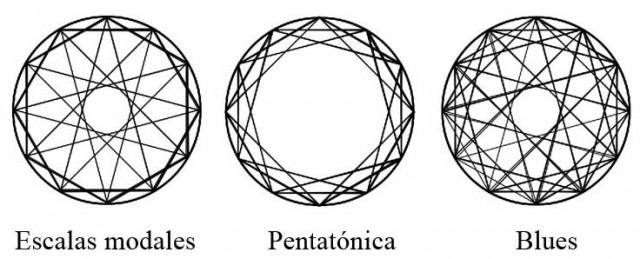 Este tipo de simetrías rotacionales son bien conocidas; lo interesante de nuestro sistema de construcción es saber de dónde parten. Se puede reconocer a simple vista que la escala de Blues tiene una extensión X(e) muy grande, mientras que la escala Pentatónica tiene una muy reducida. Las escalas modales tienen una extensión intermedia.
Este tipo de simetrías rotacionales son bien conocidas; lo interesante de nuestro sistema de construcción es saber de dónde parten. Se puede reconocer a simple vista que la escala de Blues tiene una extensión X(e) muy grande, mientras que la escala Pentatónica tiene una muy reducida. Las escalas modales tienen una extensión intermedia.
Aquí cabría hacer la siguiente pregunta:
1- ¿Cuál es la relación entre las escalas físicas y su extensión X(e)?
Pareciera no haber mucho más de forma inmediata, pero si nos ponemos a jugar el tiempo suficiente, podemos encontrar cosas sorprendentes en las rotaciones, que descubren relaciones nuevas entre las estructuras que las forman. Por ejemplo, aquí están tres escalas que ya vimos antes:
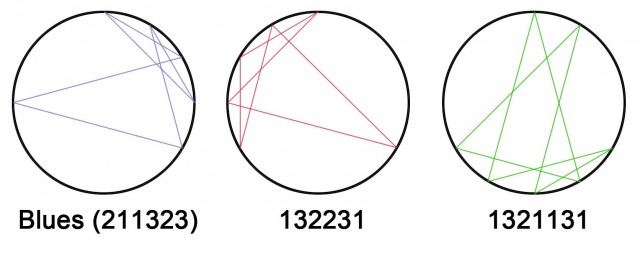 La escala de Blues, que no es simétrica; una escala con simetría arbitraria 132231; y finalmente esa misma escala pero rompiendo su simetría, cambiando el segundo 2 por dos intervalos de 1. No tienen aparentemente nada que ver entre sí.
La escala de Blues, que no es simétrica; una escala con simetría arbitraria 132231; y finalmente esa misma escala pero rompiendo su simetría, cambiando el segundo 2 por dos intervalos de 1. No tienen aparentemente nada que ver entre sí.
Eso es, hasta que las ponemos juntas en un solo diagrama:
 que a simple vista parece confuso, pero que si lo rotamos dos veces a 90 grados, nos da:
que a simple vista parece confuso, pero que si lo rotamos dos veces a 90 grados, nos da:
 …la rotación completa de la Escala de Blues. Y no sólo eso, sino que si tomamos de forma independiente a las dos escalas 132231 y 1321131 y generamos las rotaciones completas, obtenemos:
…la rotación completa de la Escala de Blues. Y no sólo eso, sino que si tomamos de forma independiente a las dos escalas 132231 y 1321131 y generamos las rotaciones completas, obtenemos:
 … de nuevo la rotación completa de Blues.
… de nuevo la rotación completa de Blues.
Las escalas no están relacionadas entre sí en el “mundo real”, por así decirlo. De hecho, las dos fueron creadas de forma «armónicamente arbitraria», tomando sólo en consideración una de varias posibles simetrías de intervalos (en este caso 132231) y una ruptura de simetría (1321131). La característica que las une es el uso del cromatismo: todas tienen por lo menos una sección con intervalos consecutivos de la forma “1 1”: dos de ellas dentro de su propia estructura, y otra al ser reproducida hacia arriba y hacia abajo. Sus polígonos de escala P(e), son radicalmente diferentes pero son Equivalentes en Rotación.
La Conjetura (2), entonces, es ésta: existe un número arbitrariamente grande de escalas que al ser diagramadas en el sistema de Círculo de Quintas, no son equivalentes en sus polígonos P(e), pero son Equivalentes en Rotación.
Esta segunda conjetura nos presenta un problema que hemos estado arrastrando a lo largo de este ensayo y que debemos reconocer aquí: las escalas a las que nos hemos estado refiriendo parten todas de los fenómenos físicos de la acústica primero y de la teoría musical después. Pero hemos dicho que al entrar en nuestro sistema, pasan a ser objetos puramente geométricos. Esto es, sus notas pasan a ser puntos y sus manipulaciones no tendrán necesariamente una equivalencia acústica o musical. Desde luego, las preguntas que nos hemos hecho a lo largo de esta investigación son muchas veces del tipo, “¿Qué pasa si traduzco de nuevo este hecho geométrico al plano físico?”, pero para poder generalizar nuestro enfoque, tendremos que considerar la totalidad de escalas posibles, y tomar las escalas musicales que hemos visto tan sólo como un subconjunto de tales patrones. Esto nos lleva a la siguiente sección, en donde trataremos de hacer una formalización sencilla de tal universo de patrones, antes de continuar con nuestros experimentos.
Siguiente: una formalización del círculo musical como espacio gráfico.
Nací en México y vivo en China desde el 2000, donde estudié idioma e historia, y luego fui investigador visitante en el Centro Internacional Wan Lin Jiang de Economía y Finanzas, así como profesor de economía e historia para extranjeros en la Universidad de Zhejiang. Actualmente dirijo el Mexico-China Center y doy conferencias acerca de ciencia y cooperación tecnológica internacional.
