 Decíamos que en nuestro sistema de graficar melodías musicales, la mayor parte de sus características distintivas desaparecen, y tan sólo nos quedamos con las figuras creadas por los movimientos entre nota y nota. Dejamos de lado duraciones, volumen y todo tipo de matices. En un sistema más sutilmente definido, en el futuro podemos tomar estos factores en consideración, pero por el momento nuestro sistema se concentra únicamente en los «saltos» entre las notas. Esto es, en las soluciones a lo que hemos definido como Conjuntos M.
Decíamos que en nuestro sistema de graficar melodías musicales, la mayor parte de sus características distintivas desaparecen, y tan sólo nos quedamos con las figuras creadas por los movimientos entre nota y nota. Dejamos de lado duraciones, volumen y todo tipo de matices. En un sistema más sutilmente definido, en el futuro podemos tomar estos factores en consideración, pero por el momento nuestro sistema se concentra únicamente en los «saltos» entre las notas. Esto es, en las soluciones a lo que hemos definido como Conjuntos M.
Por ejemplo, veamos la melodía de la famosa canción Yesterday, de The Beatles:
 Tomemos la primera frase de la melodía: “Yesterday, all my troubles seem so far away”, que en la partitura de arriba va desde el símbolo A encerrado en un cuadrado en la primera línea, hasta el acorde D-/C en la segunda línea. Si contamos, son 12 notas las que componen esta frase melódica, dos de ellas repetidas. Tomando esta frase y expresándola en nuestro espacio M, tenemos una primera figura:
Tomemos la primera frase de la melodía: “Yesterday, all my troubles seem so far away”, que en la partitura de arriba va desde el símbolo A encerrado en un cuadrado en la primera línea, hasta el acorde D-/C en la segunda línea. Si contamos, son 12 notas las que componen esta frase melódica, dos de ellas repetidas. Tomando esta frase y expresándola en nuestro espacio M, tenemos una primera figura:
 La segunda frase, “Now it looks as though they’re here to stay/Oh I believe in yesterday”, va del acorde marcado B♭ (segunda línea) hasta el final de la tercera línea (acorde de F), y tiene 16 notas también con repeticiones. Si le confunde que tomemos 16 y no 19, es porque en dos ocasiones las notas simplemente se alargan, pero están notadas de forma que parecen notas extras pero no lo son: esto pasa en el primer y el último compás del renglón 3, notado por una especie de “U” alargada, en la parte inferior de las notas que extienden su duración.
La segunda frase, “Now it looks as though they’re here to stay/Oh I believe in yesterday”, va del acorde marcado B♭ (segunda línea) hasta el final de la tercera línea (acorde de F), y tiene 16 notas también con repeticiones. Si le confunde que tomemos 16 y no 19, es porque en dos ocasiones las notas simplemente se alargan, pero están notadas de forma que parecen notas extras pero no lo son: esto pasa en el primer y el último compás del renglón 3, notado por una especie de “U” alargada, en la parte inferior de las notas que extienden su duración.
Trazando, nos da esta figura:
 En términos de nuestro sistema, son soluciones a M (12, 7) y M (16, 7), respectivamente: cómo hacer una melodía de 12 notas de extensión usando sólo 7 notas distintas, y cómo hacer una de 16 usando también 7. Poniéndolas juntas, tenemos:
En términos de nuestro sistema, son soluciones a M (12, 7) y M (16, 7), respectivamente: cómo hacer una melodía de 12 notas de extensión usando sólo 7 notas distintas, y cómo hacer una de 16 usando también 7. Poniéndolas juntas, tenemos:
 Esto es, una solución a M (28, 9): una melodía de 28 pasos, con 9 puntos distintos.
Esto es, una solución a M (28, 9): una melodía de 28 pasos, con 9 puntos distintos.
Pasemos ahora a otra melodía igualmente famosa, la Oda a la Alegría de Beethoven:
 A simple vista podemos notar que es una melodía mucho más sencilla y no tiene alteraciones (sostenidos ♯ ni bemoles ♭), por lo que sería de esperar que su extensión X(e) sea menor que la de Yesterday. Graficando en tres partes (renglón 1, renglón 2, y renglones 3 y 4), descubrimos que en efecto es éste el caso:
A simple vista podemos notar que es una melodía mucho más sencilla y no tiene alteraciones (sostenidos ♯ ni bemoles ♭), por lo que sería de esperar que su extensión X(e) sea menor que la de Yesterday. Graficando en tres partes (renglón 1, renglón 2, y renglones 3 y 4), descubrimos que en efecto es éste el caso:
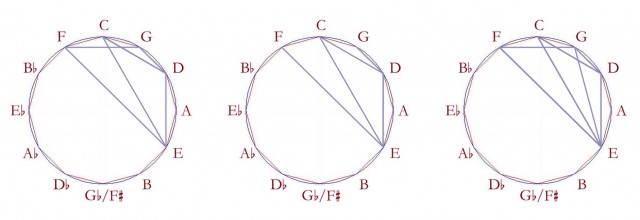 De hecho, al poner las tres partes juntas, obtenemos la tercera figura; esta es una solución a M (62, 6): una melodía de 62 pasos usando sólo 6 notas.
De hecho, al poner las tres partes juntas, obtenemos la tercera figura; esta es una solución a M (62, 6): una melodía de 62 pasos usando sólo 6 notas.
Propuesta (1):
Para abrir un campo de estudio sobre melodías y sus características en el espacio M, debemos por supuesto definir restricciones que hagan que las soluciones sigan teniendo sentido. Nuestro sistema permite una función M (100.000, 2), pero las soluciones no serían más que distintos intervalos repetidos ad nauseam. Desde luego, se requiere el uso extensivo de fuerza computacional para poder realizar un análisis de este tipo: primeramente en la creación de un archivo de piezas musicales de todo tipo de género; analizar sus melodías para definir un límite máximo para p en M (p, n); y finalmente para trazar y analizar las características de las figuras resultantes, así como crear rotaciones, reflejos, composiciones de figuras y otras funciones geométricas.
Preguntas:
- En un análisis extensivo de melodías “del mundo real”, ¿jugaría un papel importante la relación p/n (número de pasos que componen la melodía, dividido entre el número de notas distintas usadas) como clasificador?
- Además de las características que ya hemos mencionado como amplitud, extensión, orientación y ahora la relación (p/n), ¿qué otra característica sería relevante para la caracterización de melodías?
- ¿Tendría la simetría un papel relevante o incidental en la creación de melodías reales?
Con estas preguntas, terminamos nuestra breve exploración de lo que hemos definido como espacio M y de los patrones reales (escalas, acordes y melodías) que podemos considerar para mapearlos en nuestro sistema. En los siguientes capítulos propondremos manipulaciones y juegos geométricos más estrafalarios y haremos una breve reflexión acerca de sus resultados y de cómo podrían aplicarse en configuraciones distintas a las escalas musicales, que son las únicas que nos han ocupado hasta este momento.
Siguiente: jugando como locos en el Universo M.
Nací en México y vivo en China desde el 2000, donde estudié idioma e historia, y luego fui investigador visitante en el Centro Internacional Wan Lin Jiang de Economía y Finanzas, así como profesor de economía e historia para extranjeros en la Universidad de Zhejiang. Actualmente dirijo el Mexico-China Center y doy conferencias acerca de ciencia y cooperación tecnológica internacional.
