 14. JUEGOS GEOMÉTRICOS EN UN ESPACIO M
14. JUEGOS GEOMÉTRICOS EN UN ESPACIO M
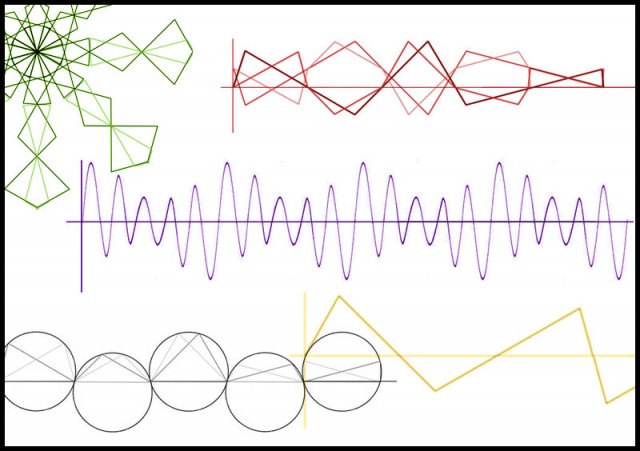
En este capítulo, siempre con el espíritu de «vamos a ver qué pasa» con el que empezamos nuestra aventura, presentaremos algunas manipulaciones geométricas básicas, para usar en las figuras que hemos ido encontrando al mapear escalas y acordes musicales. Consideremos primero el conjunto de 5 pares de triángulos que encontramos en el capítulo 13. Para nuestros propósitos, tomaremos los pares de triángulos y unificaremos sus orientaciones, colocándolos todos en simetría vertical. Esto nos da:
 Ahora los arreglamos de nuevo, poniéndolos en una misma línea base que corresponda con la base de cada figura dentro de su círculo, para formar una línea continua. Esto es:
Ahora los arreglamos de nuevo, poniéndolos en una misma línea base que corresponda con la base de cada figura dentro de su círculo, para formar una línea continua. Esto es:
 En esta primera manipulación, vemos que además de la línea base horizontal, los triángulos forman dos líneas continuas emergentes. Los triángulos 1-5 están representados en negro mientras que sus simétricos 6-10 están representados con gris. Si tomamos en cuenta cada línea de forma independiente, tenemos dos gráficas simples resultantes para los triángulos 1-5 (negros), y para sus contrapartes simétricas 6-10 (rojos):
En esta primera manipulación, vemos que además de la línea base horizontal, los triángulos forman dos líneas continuas emergentes. Los triángulos 1-5 están representados en negro mientras que sus simétricos 6-10 están representados con gris. Si tomamos en cuenta cada línea de forma independiente, tenemos dos gráficas simples resultantes para los triángulos 1-5 (negros), y para sus contrapartes simétricas 6-10 (rojos):
 No nos dice mucho, pero esta es una primera opción de manipulación. Veamos otra que pudiera ser más interesante. Cuando primero generamos los pares de triángulos, con su orientación original, obtuvimos esto:
No nos dice mucho, pero esta es una primera opción de manipulación. Veamos otra que pudiera ser más interesante. Cuando primero generamos los pares de triángulos, con su orientación original, obtuvimos esto:
 Algo que salta a la vista es que en esta generación “natural” de los pares, hay una alternancia en su orientación, haciendo que parezcan oscilar de derecha a izquierda. Tomando esto en consideración, creemos una nueva línea base para colocarlos juntos de nuevo, usando esta alternancia:
Algo que salta a la vista es que en esta generación “natural” de los pares, hay una alternancia en su orientación, haciendo que parezcan oscilar de derecha a izquierda. Tomando esto en consideración, creemos una nueva línea base para colocarlos juntos de nuevo, usando esta alternancia:
 Aquí reconocemos un obvio patrón oscilatorio al observar las líneas continuas que emergen de un círculo a otro. Yendo por este camino, podemos tomar en cuenta tres diferentes patrones: el de las líneas oscuras, el de las líneas claras, y los puntos medios:
Aquí reconocemos un obvio patrón oscilatorio al observar las líneas continuas que emergen de un círculo a otro. Yendo por este camino, podemos tomar en cuenta tres diferentes patrones: el de las líneas oscuras, el de las líneas claras, y los puntos medios:
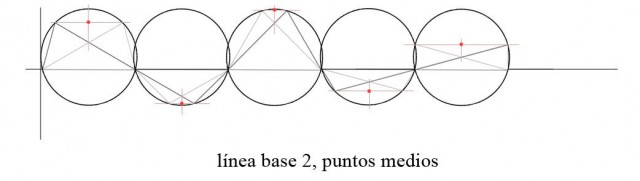 Con esta nueva disposición, podemos obtener dos nuevas líneas simples a partir de los triángulos y sus pares simétricos:
Con esta nueva disposición, podemos obtener dos nuevas líneas simples a partir de los triángulos y sus pares simétricos:
 Y como parte de nuestras manipulaciones, podemos superponer ambas líneas y reflejarlas en el eje horizontal:
Y como parte de nuestras manipulaciones, podemos superponer ambas líneas y reflejarlas en el eje horizontal:
 Ahora bien, tomando en cuenta los puntos medios de las figuras, podemos trazar una curva sinusoidal para aproximarlos:
Ahora bien, tomando en cuenta los puntos medios de las figuras, podemos trazar una curva sinusoidal para aproximarlos:
 Si la re-arreglamos para que la oscilación vaya de mayor a menor, tenemos una curva que parece la típica gráfica del movimiento armónico simple, atenuado:
Si la re-arreglamos para que la oscilación vaya de mayor a menor, tenemos una curva que parece la típica gráfica del movimiento armónico simple, atenuado:
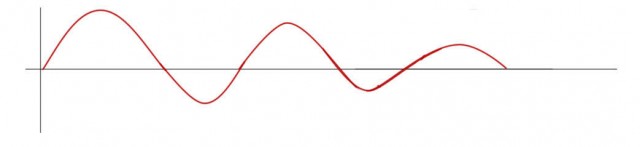 Y si queremos podemos tomar esta curva y reproducirla, aumentando su frecuencia:
Y si queremos podemos tomar esta curva y reproducirla, aumentando su frecuencia:
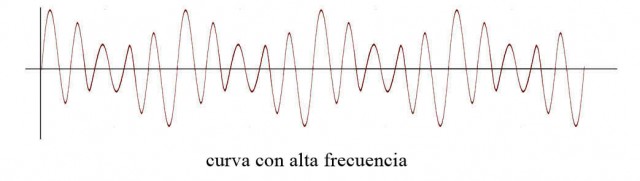 Otra opción puede ser, separar los pares de modo que obtengamos sólo líneas continuas, no rotas. Esto sería una tercera línea base y nos daría dos nuevas gráficas cuyas líneas no se rompen entre un círculo y otro:
Otra opción puede ser, separar los pares de modo que obtengamos sólo líneas continuas, no rotas. Esto sería una tercera línea base y nos daría dos nuevas gráficas cuyas líneas no se rompen entre un círculo y otro:
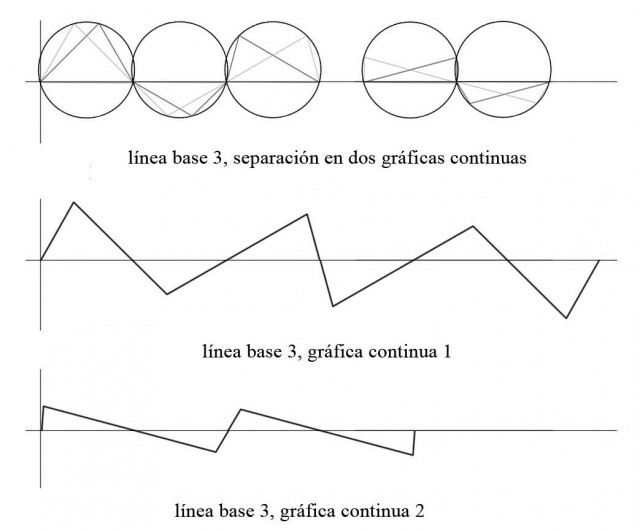 y que de nuevo podemos superponer y reflejar en el eje horizontal:
y que de nuevo podemos superponer y reflejar en el eje horizontal:
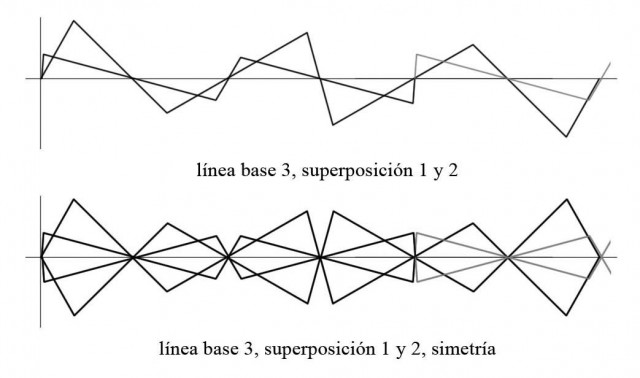 Más aún, podemos usar estas construcciones reflejadas, para rotarlas y explorar sus simetrías resultantes:
Más aún, podemos usar estas construcciones reflejadas, para rotarlas y explorar sus simetrías resultantes:
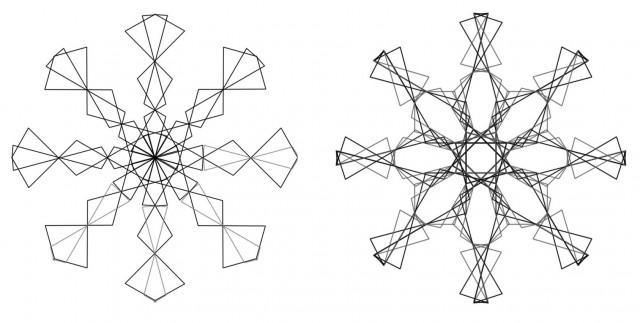 Si el lector está desconcertado por las extrañas manipulaciones de esta sección, quiero recordarle que durante toda esta exploración no debemos perder de vista el enfoque de juego y de continuamente preguntarnos, “¿qué pasa si…?”
Si el lector está desconcertado por las extrañas manipulaciones de esta sección, quiero recordarle que durante toda esta exploración no debemos perder de vista el enfoque de juego y de continuamente preguntarnos, “¿qué pasa si…?”
Otras preguntas:
- ¿Qué pasa si tomamos las gráficas de frecuencia encontradas a partir de un conjunto de pares y las llevamos “de regreso al mundo real? ¿A qué equivalen en acústica? ¿A qué equivalen en un péndulo simple? ¿Podemos relacionar las gráficas halladas con estas manipulaciones geométricas con un fenómeno físico relacionado con las escalas que usamos como datos de entrada?
- ¿Qué pasa si llevamos las gráficas de superposiciones y de rotaciones a una dimensión extra; por ejemplo en esferas, toroides y otros planos curvos? ¿Qué pasa si los generalizamos a n dimensiones?
- ¿Podemos hacer otras manipulaciones geométricas con los pares y sus gráficas simples, para obtener nuevas gráficas complejas?
- ¿Qué pasa si analizamos estas figuras emergentes usando geometría proyectiva, esto es, con manipulaciones distorsionantes?
Habiendo terminado esta sección de ejemplos de manipulación, procedamos a aplicarlos a nuestro experimento principal: las figuras basadas en escalas de siete notas.
Siguiente: Manipulando los polígonos musicales.
Nací en México y vivo en China desde el 2000, donde estudié idioma e historia, y luego fui investigador visitante en el Centro Internacional Wan Lin Jiang de Economía y Finanzas, así como profesor de economía e historia para extranjeros en la Universidad de Zhejiang. Actualmente dirijo el Mexico-China Center y doy conferencias acerca de ciencia y cooperación tecnológica internacional.
