 7. ESCALAS, PARTE III: asimetrías
7. ESCALAS, PARTE III: asimetrías
Veamos ahora unos cuantos ejemplos de escalas cuyas estructuras son asimétricas y de las cuales decimos que acústicamente crean efectos más “alejados de lo clásico” que las escalas modales:
NOMBRE – ESTRUCTURA
Menor armónica – 2 1 2 2 1 2 1
Escala de Blues – 2 1 1 3 2 3
Escala japonesa – 2 1 4 1 4
Simetría rota – 1 3 2 1 1 3 1
 Estas escalas, que incluyen intervalos grandes como la japonesa, o bien intervalos consecutivos de semitonos como la de blues, crean efectos acústicos que son comúnmente llamados “más ricos” —o simplemente más modernos— que las escalas mayor y menor. Este efecto es tanto porque estamos expuestos a ellas en menor medida que las escalas comunes, como porque rompen la simetría del polígono P(e) que crean y aumentan su amplitud A(e); esto es, se van a “pasear” armónicamente más lejos que las escalas comunes.
Estas escalas, que incluyen intervalos grandes como la japonesa, o bien intervalos consecutivos de semitonos como la de blues, crean efectos acústicos que son comúnmente llamados “más ricos” —o simplemente más modernos— que las escalas mayor y menor. Este efecto es tanto porque estamos expuestos a ellas en menor medida que las escalas comunes, como porque rompen la simetría del polígono P(e) que crean y aumentan su amplitud A(e); esto es, se van a “pasear” armónicamente más lejos que las escalas comunes.
Hay algo que podemos observar inmediatamente: en todas ellas sólo hay una nota que “rompe” la simetría. En la menor armónica, si pasara directamente de D a F (sin usar E♭) tendríamos un bella figura simétrica. Lo mismo pasa si en la japonesa cambiásemos la C por F, obteniendo una estrella simétrica en lugar de la estrella distorsionada que tenemos. Para la escala de Blues, sería pasar de E a F, en lugar de E a E♭; incluso en la extraña escala que construí numéricamente, la única nota ofensiva para la simetría es E, eliminándola tendríamos también una figura simétrica. Por supuesto, haciendo esto y aplicándolo al piano o la guitarra, seguramente destruiremos el sabor propio de todas estas escalas, pero por otro lado encontraremos patrones nuevos de una manera poco común.
(Si mi lector es músico, no espere ni un momento y compruebe en su instrumento estas cavilaciones).
Por otra parte, la escala básica de Blues mostrada arriba tiene una peculiaridad más, que ya observamos en el ejemplo del capítulo anterior: si reorientamos su estructura alrededor del círculo, adoptará nombres distintos en otros contextos, como por ejemplo Pentatónica Menor ó Escala Egipcia.
Preguntas:
- ¿Cómo se pueden calcular las áreas de estos polígonos y estrellas irregulares?
- ¿Cuál es la relación entre las áreas de estos polígonos, y las de los polígonos emergentes si eliminamos las notas necesarias para hacerlos simétricos? Esto es, hay una relación constante entre A(e) de una escala de este tipo, y el A(e) de su figura “simetrizada”? ¿Y qué tal acerca de las dispersiones D(e) de ambos?
8. DIBUJANDO ACORDES
Pasemos ahora a la otra parte fundamental de nuestras estructuras: los acordes, que son notas tocadas de forma simultánea. Para simplificar, nos limitaremos a ver acordes formados con tres, cuatro y cinco notas como máximo. A continuación una lista de los acordes que usaremos, con su notación, su nombre y las notas que lo componen:
 Como veíamos en el capítulo 2, los acordes básicos se componen con la nota fundamental y las notas que crean armónicos (frecuencias relacionadas) sobre ellas. El acorde más básico es Do Mayor, formado por Do-Mi-Sol, que son los grados I-III-V de la escala. Los nombres de los acordes arriba pueden parecerle exóticos, pero simplemente están indicando qué notas extras o notas enfáticas están agregando. Por ejemplo, C6 quiere decir que al acorde de Do, le agregamos su sexto grado: la nota La.
Como veíamos en el capítulo 2, los acordes básicos se componen con la nota fundamental y las notas que crean armónicos (frecuencias relacionadas) sobre ellas. El acorde más básico es Do Mayor, formado por Do-Mi-Sol, que son los grados I-III-V de la escala. Los nombres de los acordes arriba pueden parecerle exóticos, pero simplemente están indicando qué notas extras o notas enfáticas están agregando. Por ejemplo, C6 quiere decir que al acorde de Do, le agregamos su sexto grado: la nota La.
Quizá el nombre que le suene más extraño al lector sea el de “Do suspendido”: quiere decir que el acorde no tiene en su estructura a la Mediante (grado III), que normalmente es la que define si estamos escuchando un acorde mayor o menor. Sin esta mediante, el acorde se queda un poco en el limbo, o “suspendido”.
Puede haber otra causa de confusión en los últimos dos miembros de la tercera columna, donde se indican las notas de cada acorde. Se preguntará porqué en C9sus4, la última nota es D (Re), en vez de aparecer entre Do y Mi, que es donde está en la escala. La respuesta es que las notas adicionales que sobrepasan la octava —por ejemplo 9 y 11— se añaden arriba de las notas del acorde. Así que la lógica del acorde no sigue necesariamente la convención de la escala, que son siempre notas sucesivas tal y como están en las teclas del piano.
Veamos cuáles son los resultados. De la misma forma que con las escalas, hallamos tanto acordes que presentan figuras regulares (simétricas):
como irregulares:
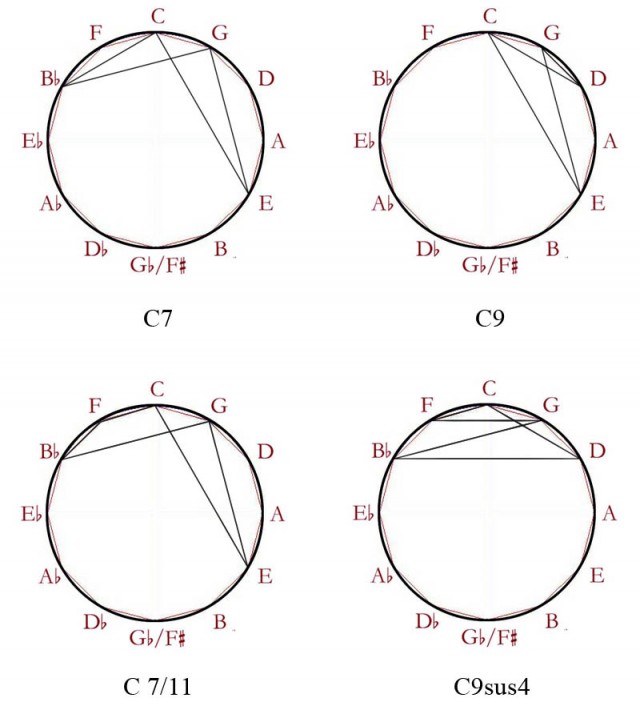 Una cosa salta a la vista en la primera ilustración (círculo inferior a la derecha), donde pongo juntos en un mismo círculo las figuras creadas por Cmaj7 y Cm7: es una pseudo-simetría en la que el acorde menor es un reflejo del mayor, pero con menor amplitud.
Una cosa salta a la vista en la primera ilustración (círculo inferior a la derecha), donde pongo juntos en un mismo círculo las figuras creadas por Cmaj7 y Cm7: es una pseudo-simetría en la que el acorde menor es un reflejo del mayor, pero con menor amplitud.
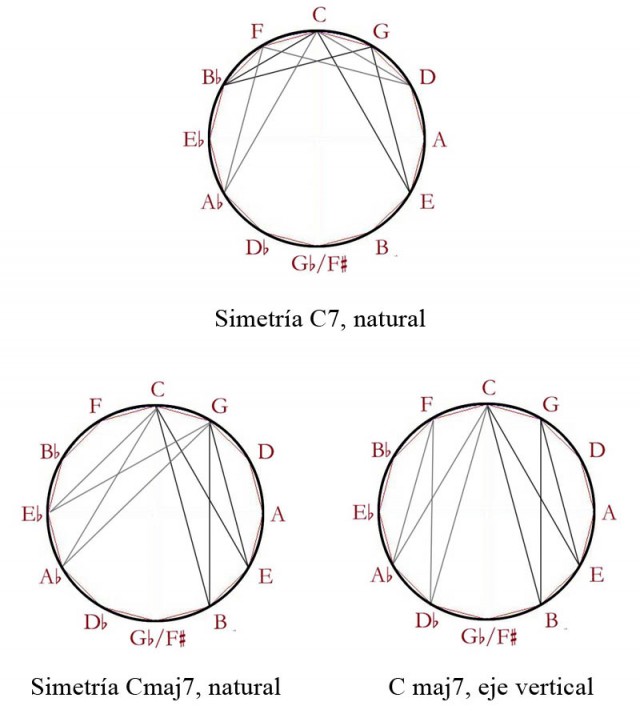
Se preguntará por qué no incluyo los dos acordes más importantes: el mayor y el menor. Pues bien, he aquí la sorpresa de que si en música constituyen la diferencia más importante en la percepción de una pieza, en nuestra geometría son indistinguibles salvo por su Orientación:
 En el círculo superior he sobrepuesto los acordes de Do Mayor (negro) y Do Menor (gris) para mostrar su simetría. En el primer círculo inferior he tomado el triángulo resultante, rotándolo para obtener una simetría vertical. En el segundo, he invertido ambos triángulos. Así, uno de los vértices de cada triángulo siempre está en C y encontramos con este juego, nuevos acordes que son, en nuestro sistema, equivalentes: Fm, C6 y Fm7. Podemos obtener resultados más complejos pero de la misma naturaleza, jugando con acordes de cuatro notas:
En el círculo superior he sobrepuesto los acordes de Do Mayor (negro) y Do Menor (gris) para mostrar su simetría. En el primer círculo inferior he tomado el triángulo resultante, rotándolo para obtener una simetría vertical. En el segundo, he invertido ambos triángulos. Así, uno de los vértices de cada triángulo siempre está en C y encontramos con este juego, nuevos acordes que son, en nuestro sistema, equivalentes: Fm, C6 y Fm7. Podemos obtener resultados más complejos pero de la misma naturaleza, jugando con acordes de cuatro notas:
 Además, de la misa forma que en el capítulo VII inventé una escala basado simplemente en consideraciones de simetría de intervalos, podemos jugar construyendo acordes basados únicamente en geometría. Aquí ejemplos de acordes de tres y cuatro notas, que emergen a partir de triángulos y cuadrángulos con simetría en la vertical:
Además, de la misa forma que en el capítulo VII inventé una escala basado simplemente en consideraciones de simetría de intervalos, podemos jugar construyendo acordes basados únicamente en geometría. Aquí ejemplos de acordes de tres y cuatro notas, que emergen a partir de triángulos y cuadrángulos con simetría en la vertical:
- ¿Existe una relación entre la simetría del sistema y las consonancias armónicas reales? Si hemos dicho que a medida que aumenta la amplitud del polígono aumenta la disonancia, ¿es ésta una relación estrictamente inversa?
- ¿Qué consecuencias armónicas reales tienen la rotación y las inversiones geométricas de figuras en el sistema?¿Es predecible la relación?
9. CONSTRUCCIONES EN UN CÍRCULO CROMÁTICO
Cuando dijimos en el capítulo 2 que el Círculo de Quintas proporciona una estructura interesante para la construcción de un sistema de geometría, no dijimos que fuera el único ni que fuera óptimo. Los resultados que hemos obtenido graficando de manera básica algunas escalas y acordes son interesantes, pero hay otras opciones que se pueden considerar. Una opción obvia sería arreglar en el dodecágono las doce notas de la escala, pero usando el intervalo que de hecho existe entre ellas: un semitono. Nuestro círculo entonces sería un Círculo Cromático: las notas estarían arregladas alrededor en el mismo orden que se suceden en el piano.
Antes de proceder a realizar las figuras, ¿puede imaginarse cómo serían distintas de las que hemos obtenido en el Círculo de Quintas?
El resultado es mucho menos simétrico cuando empezamos a obtener los polígonos basados en escalas:
 Nada más que polígonos irregulares. E igualmente aburridas parecen ser las figuras obtenidas a partir de acordes:
Nada más que polígonos irregulares. E igualmente aburridas parecen ser las figuras obtenidas a partir de acordes:
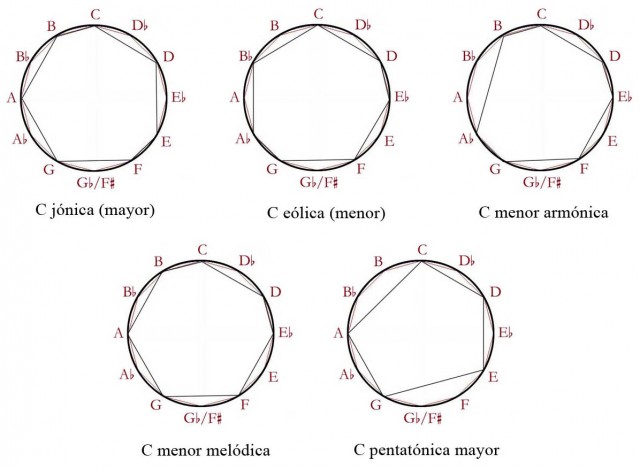
 Existen algunos casos de escalas y de acordes que presentan simetrías interesantes, e incluso relacionadas con sus pares en el Círculo de Quintas, pero parecen ser resultado de la coincidencia de la posición de sus notas integrantes en ambos círculos. Aquí vemos simetrías creadas por escalas (los tres círculos de la izquierda) y por acordes (tres círculos de la derecha):
Existen algunos casos de escalas y de acordes que presentan simetrías interesantes, e incluso relacionadas con sus pares en el Círculo de Quintas, pero parecen ser resultado de la coincidencia de la posición de sus notas integrantes en ambos círculos. Aquí vemos simetrías creadas por escalas (los tres círculos de la izquierda) y por acordes (tres círculos de la derecha):
 La respuesta parece ser obvia: la progresión de quintas es una progresión físicamente armónica: las frecuencias de hecho aparecen en el mundo y resuenan de esa manera. Por otro lado, la progresión cromática es disonante y las frecuencias con un semitono de distancia no aparecen de forma inmediata. De hecho el incluir las doce notas una tras otra en una sola escala es contrario a la aparición natural de los sobretonos: es una convención artificial para incluir en una sola secuencia todas las notas adicionales que aparecen cuando creamos todas las escalas posibles.
La respuesta parece ser obvia: la progresión de quintas es una progresión físicamente armónica: las frecuencias de hecho aparecen en el mundo y resuenan de esa manera. Por otro lado, la progresión cromática es disonante y las frecuencias con un semitono de distancia no aparecen de forma inmediata. De hecho el incluir las doce notas una tras otra en una sola escala es contrario a la aparición natural de los sobretonos: es una convención artificial para incluir en una sola secuencia todas las notas adicionales que aparecen cuando creamos todas las escalas posibles.
Mantenemos que la elección del Círculo de Quintas como marco para la construcción de nuestro sistema geométrico, si no óptimo, sí es una opción que puede interpretar de manera no trivial los fenómenos físicos originales.
La Conjetura (1), entonces, es ésta: dentro de nuestro sistema, el fenómeno acústico llamado Armonía, tiene su equivalencia en el concepto de Simetría.
Siguiente: rotaciones y la Paradoja del Blues.
Nací en México y vivo en China desde el 2000, donde estudié idioma e historia, y luego fui investigador visitante en el Centro Internacional Wan Lin Jiang de Economía y Finanzas, así como profesor de economía e historia para extranjeros en la Universidad de Zhejiang. Actualmente dirijo el Mexico-China Center y doy conferencias acerca de ciencia y cooperación tecnológica internacional.


