 15. JUEGOS GEOMÉTRICOS EN UNA FIGURA BASADA EN ESCALAS MUSICALES
15. JUEGOS GEOMÉTRICOS EN UNA FIGURA BASADA EN ESCALAS MUSICALES
En el capítulo anterior vimos varias opciones de manipulación y de observaciones que podemos hacer a las figuras construidas en nuestro espacio M. Como ejemplo, nos basamos en los pares geométricos que encontramos como una solución de lo que conocemos ya como M (3, 3). Ahora aplicaremos el mismo tipo de acciones a nuestro interés original, que son las notas musicales, o bien lo que llamamos una solución a M (7, 7). La figura que tomaremos como base de todo nuestro desarrollo será el atractivo polígono que aparece cuando trazamos en nuestro sistema las escalas modales clásicas. He aquí la figura, en su simetría vertical:
 Lo primero que haremos será crear una línea base para buscar la emergencia de líneas continuas, usando el mismo fenómeno de oscilación que vimos en el capítulo anterior:
Lo primero que haremos será crear una línea base para buscar la emergencia de líneas continuas, usando el mismo fenómeno de oscilación que vimos en el capítulo anterior:
 El lector con ojo de halcón objetará que de hecho las escalas modales nunca generan la simetría que proponemos aquí, y todas las orientaciones se concentran en la parte superior del círculo. La respuesta es: cierto, pero sólo si consideramos las escalas que parten de C. De hecho la estructura puede generarse en cualquier orientación y es por eso que he tomado su contraparte reflejada en el eje horizontal. Por supuesto, este ejercicio puede hacerse con cualquier par de orientaciones de la figura. Por el momento, procedamos con esta que se antoja más sencilla.
El lector con ojo de halcón objetará que de hecho las escalas modales nunca generan la simetría que proponemos aquí, y todas las orientaciones se concentran en la parte superior del círculo. La respuesta es: cierto, pero sólo si consideramos las escalas que parten de C. De hecho la estructura puede generarse en cualquier orientación y es por eso que he tomado su contraparte reflejada en el eje horizontal. Por supuesto, este ejercicio puede hacerse con cualquier par de orientaciones de la figura. Por el momento, procedamos con esta que se antoja más sencilla.
Otra vez, nuestra primera línea base sugiere de inmediato el comportamiento de una curva sinusoidal y además nos ofrece una gráfica continua obvia:
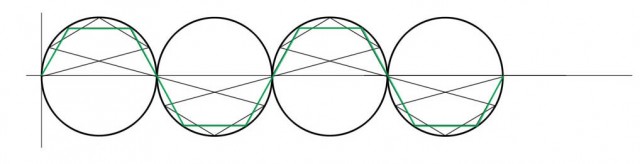
 y de hecho tenemos una segunda candidata de esta forma:
y de hecho tenemos una segunda candidata de esta forma:
pero observando con detenimiento descubrimos que en esta base, la línea no es realmente continua. Si quisiéramos representarla de esta manera de la forma indicada por la línea violeta, sería erróneo ya que el polígono no incluye la línea que asciende (mostrada sola a la extrema derecha de la gráfica). Si quisiéramos hacerla realmente continua, tendríamos que tomar los segundos dos círculos y bajarlos juntos hasta donde acaba la línea de los primeros dos. Después, tomar círculos subsecuentes e irlos bajando cada vez: esto quiere decir que la línea violeta es divergente, o sea que irá hacia abajo infinitamente. Para compensar por esto, simplemente tomemos el trazo que de hecho es continuo, interrumpirlo donde acaba, y reanudarlo de nuevo a la misma altura original. Esto es:
 Si el lector de nuevo objeta que esta solución es forzada o exótica, la respuesta es: no es forzada. Veamos la razón: cualquier punto válido en el dodecágono (o sea, cualquier punto con una nota que está dentro de nuestra escala/estructura) puede unirse con cualquier otro punto válido; de modo que si tomamos los círculos y los ponemos unos junto a otros en diferentes configuraciones, siempre será válido si el punto de contacto incluye dos puntos existentes en nuestra escala.
Si el lector de nuevo objeta que esta solución es forzada o exótica, la respuesta es: no es forzada. Veamos la razón: cualquier punto válido en el dodecágono (o sea, cualquier punto con una nota que está dentro de nuestra escala/estructura) puede unirse con cualquier otro punto válido; de modo que si tomamos los círculos y los ponemos unos junto a otros en diferentes configuraciones, siempre será válido si el punto de contacto incluye dos puntos existentes en nuestra escala.
Finalmente, la tercera parte de la figura tampoco da una gráfica continua en esta línea base. De modo que podemos crear una nueva configuración y solucionarlo:
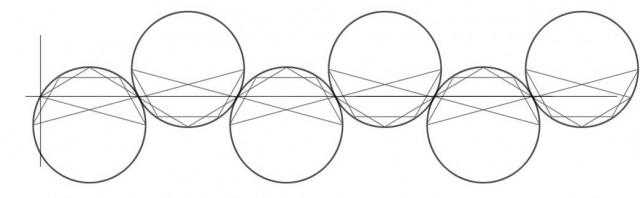
 Obteniendo la tercera gráfica continua para nuestra figura:
Obteniendo la tercera gráfica continua para nuestra figura:
 Tenemos ahora tres líneas continuas, que podemos sobreponer en una sola gráfica, junto con una curva (S) que aproxima el comportamiento de la línea 1 (L1, verde), que es obviamente sinusoidal. L1 tiene la extensión del diámetro del círculo original, de modo que coincidirá con nuestra curva S ciclo que sea múltiplo de π.
Tenemos ahora tres líneas continuas, que podemos sobreponer en una sola gráfica, junto con una curva (S) que aproxima el comportamiento de la línea 1 (L1, verde), que es obviamente sinusoidal. L1 tiene la extensión del diámetro del círculo original, de modo que coincidirá con nuestra curva S ciclo que sea múltiplo de π.
(En coordenadas cartesianas, decimos que medio círculo equivale a 1800, pero en las llamadas coordenadas polares medimos en una unidad llamada radianes. En coordenadas polares, 1800 equivalen a π radianes, el círculo completo de 3600 son 2π radianes, etc. Usaré la convención de coordenadas polares en este ejercicio).
Veamos la superposición simple de nuestras tres gráficas:
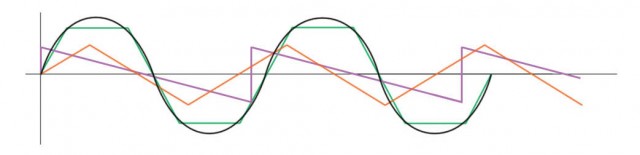 Las otras dos líneas (L2, violeta y L3, naranja) tienen una relación no muy evidente en esta representación. Pero si las movemos un poco, vemos que:
Las otras dos líneas (L2, violeta y L3, naranja) tienen una relación no muy evidente en esta representación. Pero si las movemos un poco, vemos que:
 aunque construimos L2 y L3 de formas “exóticas”, de hecho ambas predicen la amplitud de la curva S. Y si ahora las movemos para que coincidan en el origen, tenemos:
aunque construimos L2 y L3 de formas “exóticas”, de hecho ambas predicen la amplitud de la curva S. Y si ahora las movemos para que coincidan en el origen, tenemos:
 Los periodos de L2 y L3 se extienden más allá de 3π, de modo que tenemos que extender la gráfica para ver dónde coinciden:
Los periodos de L2 y L3 se extienden más allá de 3π, de modo que tenemos que extender la gráfica para ver dónde coinciden:
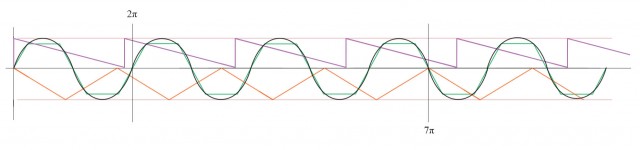 La siguiente coincidencia es 7π, en donde L3 coincide de nuevo en el origen con la curva S. L2 aún sigue desfasada, de modo que volvemos a extender y vemos, con una gráfica compactada:
La siguiente coincidencia es 7π, en donde L3 coincide de nuevo en el origen con la curva S. L2 aún sigue desfasada, de modo que volvemos a extender y vemos, con una gráfica compactada:
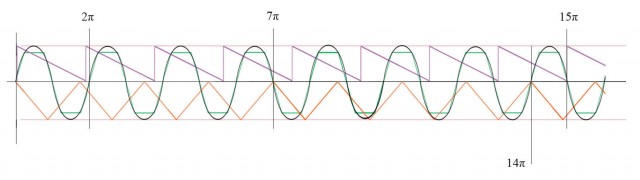 Finalmente hallamos que la coincidencia de la línea 2 es en 15π. Podemos ver también en 14π la segunda coincidencia de L1 y L2 con la curva S.
Finalmente hallamos que la coincidencia de la línea 2 es en 15π. Podemos ver también en 14π la segunda coincidencia de L1 y L2 con la curva S.
En este espacio no podemos observar la primera coincidencia de L1, L2, L3 y la curva S, que siendo el mínimo común múltiplo de las tres L, se halla en 1 x 7 x 15= 105π.
Otras observaciones que podemos hacer se refieren a las relaciones entre el ciclo de la curva S que describe el comportamiento general de nuestro polígono, y los ciclos que emergen a partir de las líneas continuas del polígono. Esto es, cuántos ciclos de S y cuántos ciclos de L1, L2 y L3 se requieren para coincidir.
En este caso:
S:L1= 1/1 = 1.0
S:L2= 7/4 = 1.75
S:L3= 15/8 = 1.875
Preguntas:
- ¿Existe una relación entre el número p —que indica la cantidad de notas de la escala a trazar— y los ciclos de coincidencia de las líneas emergentes del polígono?
- ¿Cuál es el máximo número de líneas continuas que pueden emerger de un polígono de p puntos? Llamemos a este número Lm.
- Las Lm líneas continuas de un polígono, ¿pueden coincidir siempre con una sola curva sinusoidal S? Mi Conjetura (3) es que sí, se necesita solamente una sola curva S.
- En el caso desarrollado, encontramos el mínimo punto de coincidencia de las tres líneas y la curva S en 105π. Esto lo podemos expresar como:
C(p) = π · p(2p+1) = π (2p2+p)
donde C(p) es el número de ciclos en donde todas las líneas coinciden por primera vez, expresado en radianes; y p es el grado del Conjunto M, en este caso 7.
Esta expresión, ¿es particular de este solo ejemplo, o puede ser generalizada? Y las expresiones halladas para diversas escalas, ¿pueden construir en conjunto un álgebra especial, al estilo de las sumatorias de Ramanujan?
* * *
Llegamos con esto al final de nuestra exploración de una pequeña esquina de lo que hemos denominado espacio M, y en él, de un par de casos en donde hemos creado figuras geométricas interesantes a partir de estructuras musicales. Ahora la serpiente se puede morder la cola y podemos regresar a la idea con la que empezamos todo:
El lector me podría preguntar, “pero ¿por qué hiciste todo eso?” y yo diría, “no lo sé.” Me podría decir, “pero quién va a usar eso?” y yo diría, “no lo sé.”
Siguiente: Conclusiones.
Nací en México y vivo en China desde el 2000, donde estudié idioma e historia, y luego fui investigador visitante en el Centro Internacional Wan Lin Jiang de Economía y Finanzas, así como profesor de economía e historia para extranjeros en la Universidad de Zhejiang. Actualmente dirijo el Mexico-China Center y doy conferencias acerca de ciencia y cooperación tecnológica internacional.

