 En la primera parte de Las Matemáticas Son Tus Amigas explicaba que la mayor parte del tiempo, usamos las matemáticas para “traducir el mundo”: observamos un problema complicado y lo ponemos en los términos de un lenguaje concreto y sin ambigüedades, de modo que podemos resolver esta idealización del problema, para luego tomar la solución y aplicarla (“retraducirla”) al mundo.
En la primera parte de Las Matemáticas Son Tus Amigas explicaba que la mayor parte del tiempo, usamos las matemáticas para “traducir el mundo”: observamos un problema complicado y lo ponemos en los términos de un lenguaje concreto y sin ambigüedades, de modo que podemos resolver esta idealización del problema, para luego tomar la solución y aplicarla (“retraducirla”) al mundo.
En la segunda parte decía que desde luego que eso no es todo lo que hacemos, porque siendo las matemáticas un lenguaje, en nuestros ratos de ocio y de imaginación, las usamos como los poetas o los narradores. Esto es, tomamos sus palabras y nos ponemos a jugar con ellas, mezclando conceptos y creando el equivalente de unicornios, o tomando algo conocido y dándole una nueva acepción.
En general, nos encanta tomar algún elemento conocido y decir, “a ver, ¿qué pasa si…?”
Y de esta forma a veces nos topamos con cosas inesperadas, que son las mejores de todas porque nos dan aliciente para hacer la siguiente pregunta: “¿por qué pasó esto?”
Pues bien, hoy vamos a hacer eso precisamente.
¿Cómo empezar a jugar?
Tomemos las dos cosas clásicas de las matemáticas: números y dibujos. Dentro de la teoría de números seguramente uno de los temas más interesantes son los números primos, y en geometría, el círculo es la reina de las figuras. Vayamos por ahí.
En una ocasión anterior propuse un ejercicio para representar escalas musicales en espacios circulares, con resultados muy interesantes al usar escalas griegas, jugar con las escalas de blues, graficar a Beethoven y otras locuras. Hagamos algo similar: contemos números primos en un círculo.
Comencemos por definir un decágono dentro de un círculo, y poner los 10 dígitos en sus vértices:
 Y ahora simplemente empecemos a contar números primos (por sus terminaciones) y cada vez que encontramos el siguiente, dibujamos una recta desde el inmediatamente anterior. Veamos cómo se ven nuestras primeras secuencias, digamos hasta el 300:
Y ahora simplemente empecemos a contar números primos (por sus terminaciones) y cada vez que encontramos el siguiente, dibujamos una recta desde el inmediatamente anterior. Veamos cómo se ven nuestras primeras secuencias, digamos hasta el 300:
 En el último círculo incluí un recorrido de 14 primos de forma no sobrepuesta apreciar mejor los trayectos de ida y vuelta.
En el último círculo incluí un recorrido de 14 primos de forma no sobrepuesta apreciar mejor los trayectos de ida y vuelta.
Ahora bien, ya que los primos no pueden tener más que 6 terminaciones en un espacio de 10 terminaciones posibles, obtenemos rápidamente un polígono cuasi-simétrico al que llamaremos, por falta de imaginación, Polígono Primo (Polígono P). Rotando un poco nuestro círculo para apreciarlo en su simetría vertical, tenemos:
 Nótese que la particularidad de esta figura emerge del hecho de que incluimos el 2, el único primo par y que una sola vez se mete en nuestra secuencia, pero esa vez es suficiente para crear un área extra en una figura que de otra manera sería simétrico. Veamos todas las particularidades que este bulto extra causa en nuestra figura.
Nótese que la particularidad de esta figura emerge del hecho de que incluimos el 2, el único primo par y que una sola vez se mete en nuestra secuencia, pero esa vez es suficiente para crear un área extra en una figura que de otra manera sería simétrico. Veamos todas las particularidades que este bulto extra causa en nuestra figura.
Explorando una figura nueva
Primero que nada, notamos que podemos definir tres diferentes alturas en nuestro Polígono P:
 Donde:
Donde:
h/2 es la altura media real,
l/2 es la longitud media (la mitad del segmento AC),
hV es la altura del vértice V,
hI es la altura del punto de intersección O, y
el ángulo ∠DVC es de 1440.
Esto es algo muy curioso y porque no tenemos nada mejor qué hacer, nos preguntamos:
- ¿Cuál es el área del Polígono P inscrito en un círculo de radio r=1?
- ¿Cuáles son las áreas de sus triángulos internos ABO, ADO y CDV?
- ¿Cuáles son las relaciones entre las áreas de sus triángulos internos y su área total?
- ¿Cuáles son las áreas de los polígonos internos, si lo seccionamos horizontalmente en sus tres alturas h/2, hV y hI?
- ¿Cuáles son las relaciones entre las áreas de sus polígonos internos y su área total?
Todas estas preguntas son más o menos sencillas, pero como se hacen sobre una figura poco común, nos dan para un buen rato de ejercitar nuestros conocimientos de geometría. Otra cosa muy bonita es que muchas veces un acertijo geométrico se puede resolver de más de una manera y eso ejercita nuestra imaginación para buscar métodos poco usuales, o combinaciones de métodos, para llegar a la respuesta.
Haciendo más preguntas locas
Hace tiempo ilustré un poco del bello romance que existe entre el triángulo y el círculo: esto es, teniendo una figura poligonal, ¿qué pasa si empezamos a dibujar círculos en ella? En el caso del triángulo, los resultados han dado siglos de experimentos. De modo que podemos pasar a dibujar a círculos en nuestro Polígono P y ver si otro romance parecido puede brotar.
 Primero, éstos son los cinco círculos que aparecen al tomar el centro en O. Los círculos se forman en este orden:
Primero, éstos son los cinco círculos que aparecen al tomar el centro en O. Los círculos se forman en este orden:
– al tocar el segmento AD
– al tocar el segmento BC
– al tocar los puntos A y D
– al tocar el punto V, y
– al tocar los puntos B y C.
De manera similar podemos obtener círculos a partir de los centros OV y Oh:
 Las tres opciones parecen equivalentes, pero pronto nos damos cuenta de que esto no puede ser, ya que si tomamos como origen a Oh sólo generamos cuatro círculos en vez de cinco, porque siendo la altura media real, el mismo círculo toca AD y BC al mismo tiempo. Al sobreponer los tres conjuntos de círculos en una sola imagen y ponerlos en un solo origen para más claridad, podemos apreciar que en realidad se crea un efecto de ondulación:
Las tres opciones parecen equivalentes, pero pronto nos damos cuenta de que esto no puede ser, ya que si tomamos como origen a Oh sólo generamos cuatro círculos en vez de cinco, porque siendo la altura media real, el mismo círculo toca AD y BC al mismo tiempo. Al sobreponer los tres conjuntos de círculos en una sola imagen y ponerlos en un solo origen para más claridad, podemos apreciar que en realidad se crea un efecto de ondulación:
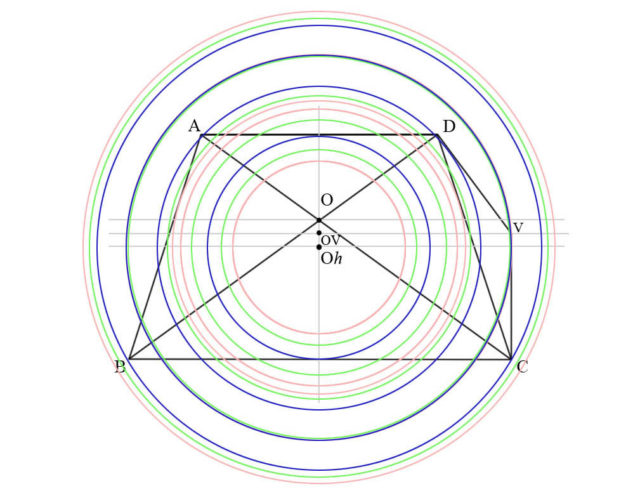 Todos los círculos son diferentes al usar diferentes centros, a excepción de los círculos que tocan el punto V, con lo que obtenemos 12 círculos en total, y no los 14 que obtendríamos al sumar 5 + 5 + 4. Además, la ondulación es irregular, con dos áreas de concentración de círculos con diámetros muy semejantes, y dos áreas con círculos con mayor diferencia entre sus diámetros.
Todos los círculos son diferentes al usar diferentes centros, a excepción de los círculos que tocan el punto V, con lo que obtenemos 12 círculos en total, y no los 14 que obtendríamos al sumar 5 + 5 + 4. Además, la ondulación es irregular, con dos áreas de concentración de círculos con diámetros muy semejantes, y dos áreas con círculos con mayor diferencia entre sus diámetros.
Más locuras aún:
- ¿Cuál es la relación entre los diámetros de los 12 círculos resultantes?
- Si creamos doce ondas sinusoidales a partir de los 12 círculos ¿cómo se comportan y cuándo coinciden?
Hay muchísimas más cosas que podemos seguir preguntándonos si seguimos dándole vueltas a nuestro Polígono P, y simplemente por el placer de hacer, nos decimos, “¿qué pasa si…?”
La imagen al principio de este artículo son tres diferentes rotaciones del Polígono P, usando diferentes puntos de rotación.
Lo hermoso de todo esto es que como mínimo, podemos divertirnos y encontrar bellas figuras y simetrías, así como ejercitar nuestros conocimientos para resolver este tipo de problemas. Y en el mejor de los casos, al encontrar la solución de uno de ellos podemos encontrar un número inesperado, una relación, o lo mejor: un patrón que no sabíamos que existía.
Esto es la poesía del pensamiento matemático.
Nací en México y vivo en China desde el 2000, donde estudié idioma e historia, y luego fui investigador visitante en el Centro Internacional Wan Lin Jiang de Economía y Finanzas, así como profesor de economía e historia para extranjeros en la Universidad de Zhejiang. Actualmente dirijo el Mexico-China Center y doy conferencias acerca de ciencia y cooperación tecnológica internacional.
